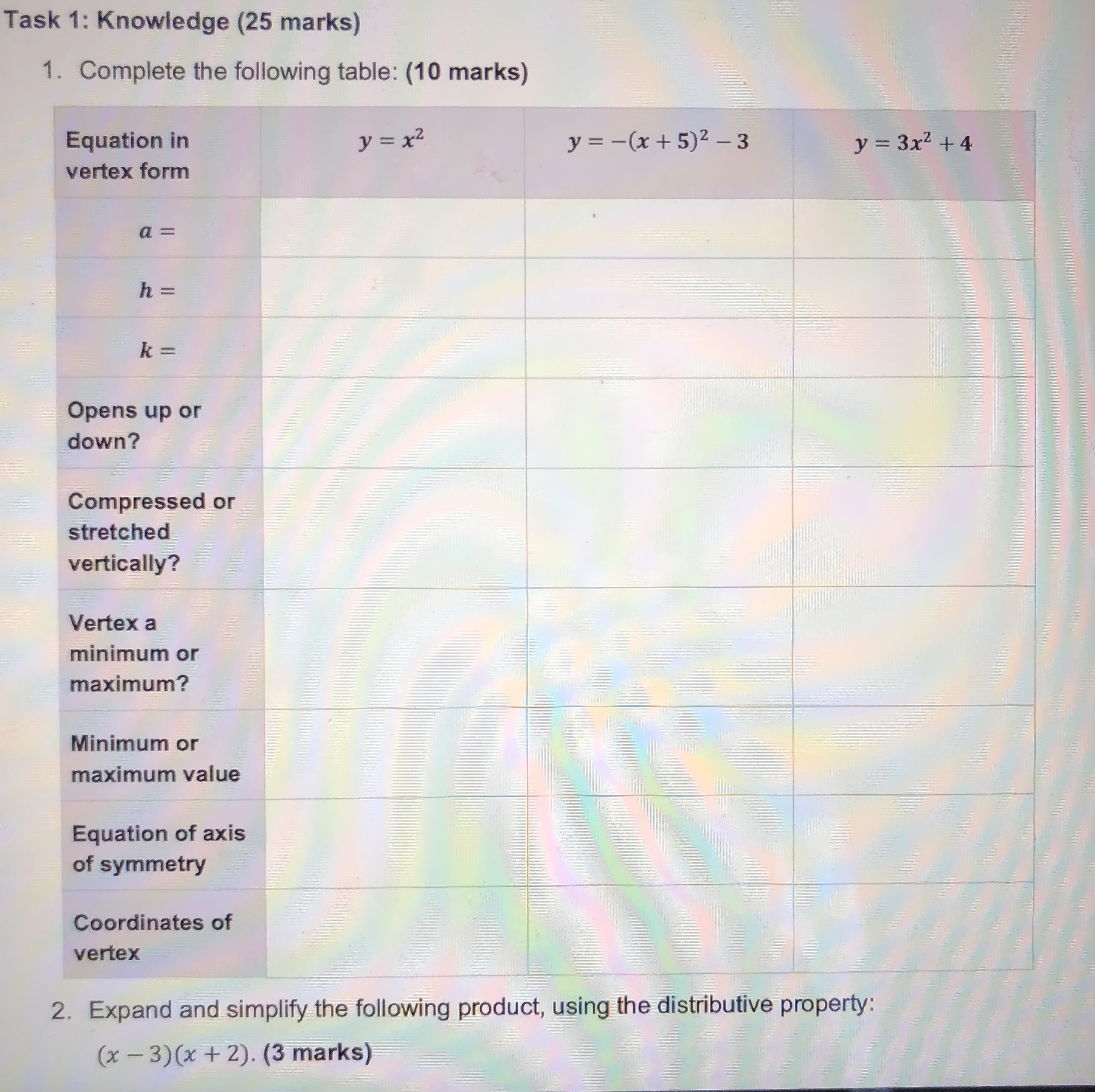
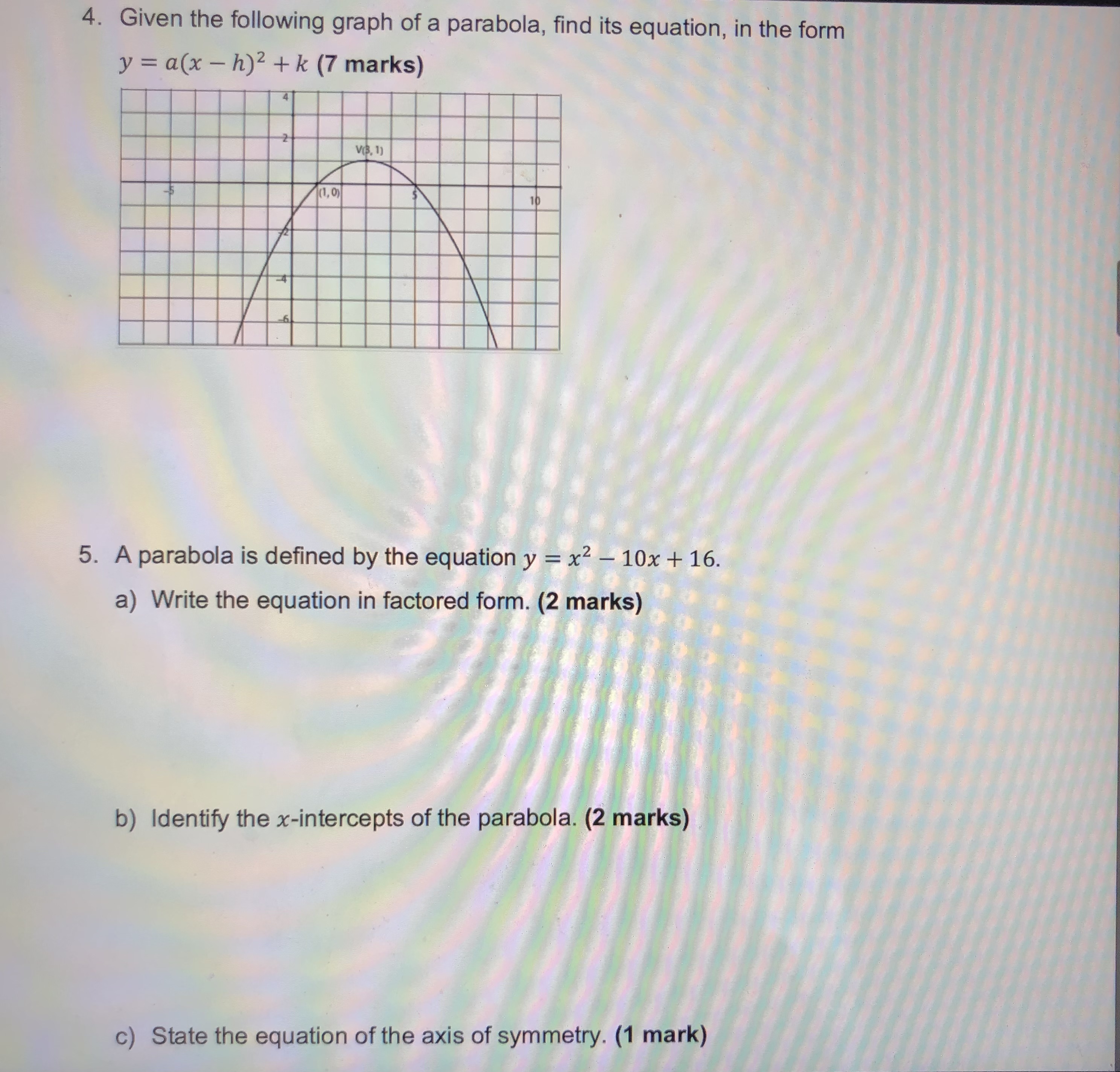
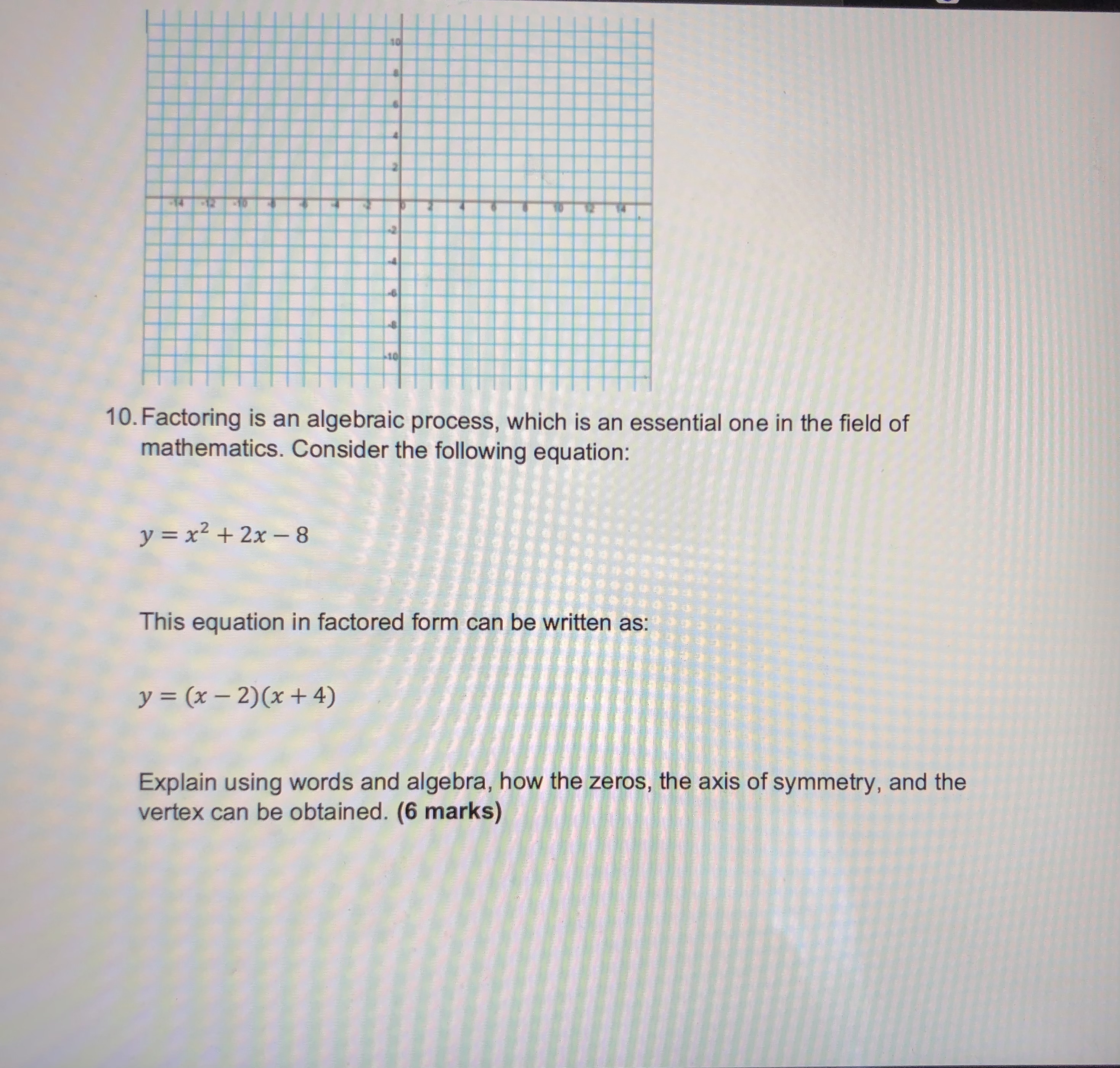
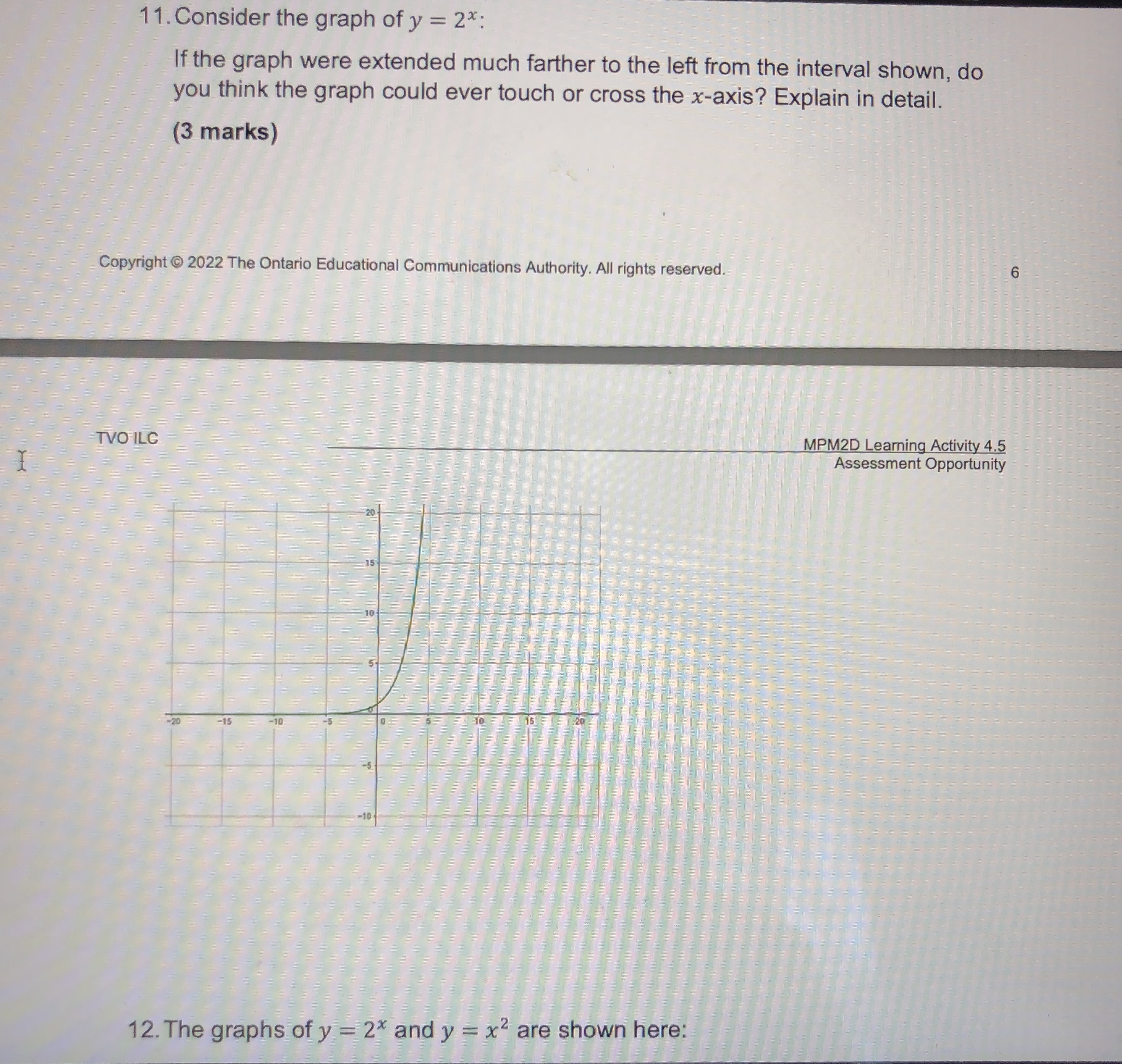
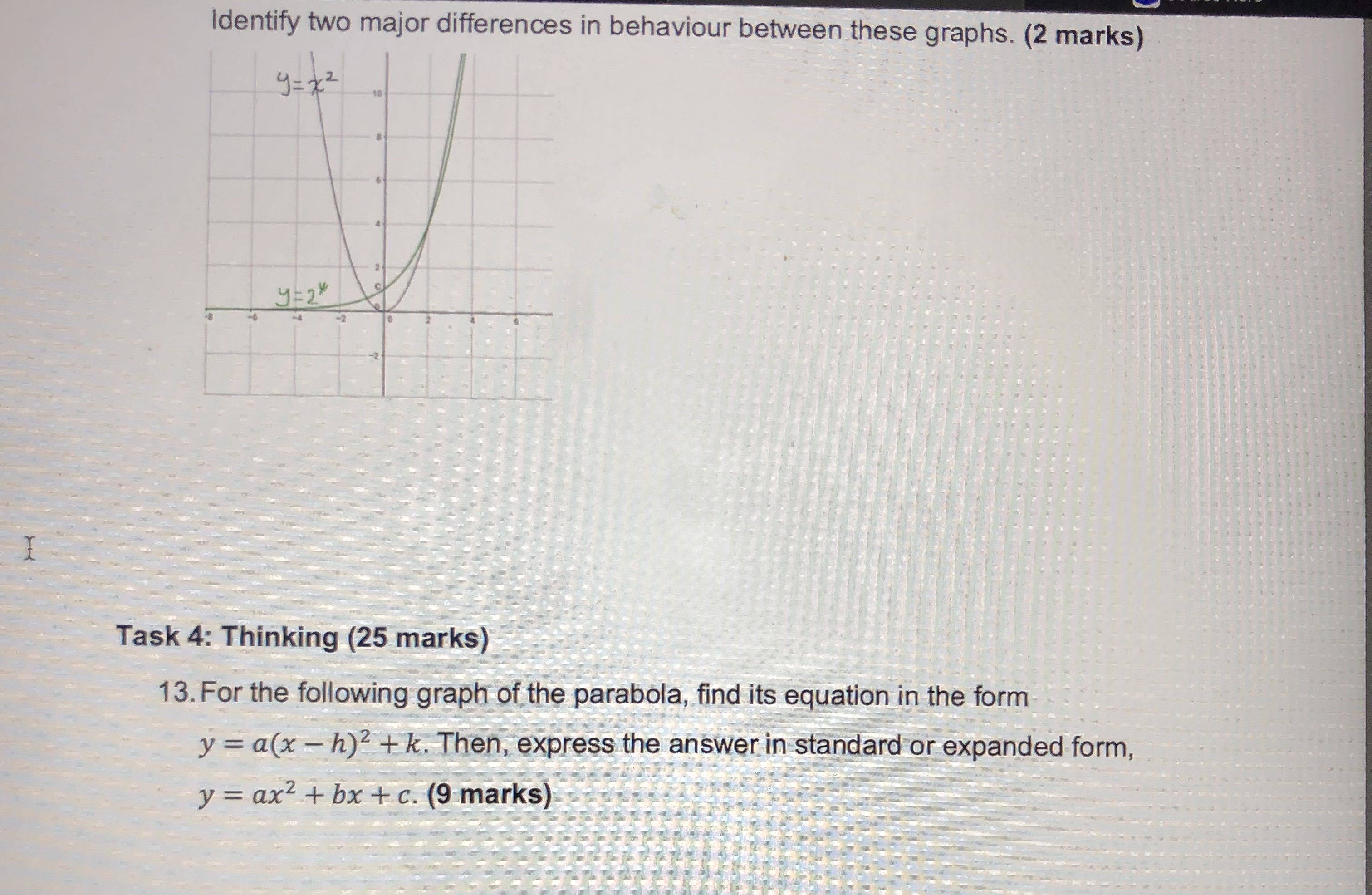
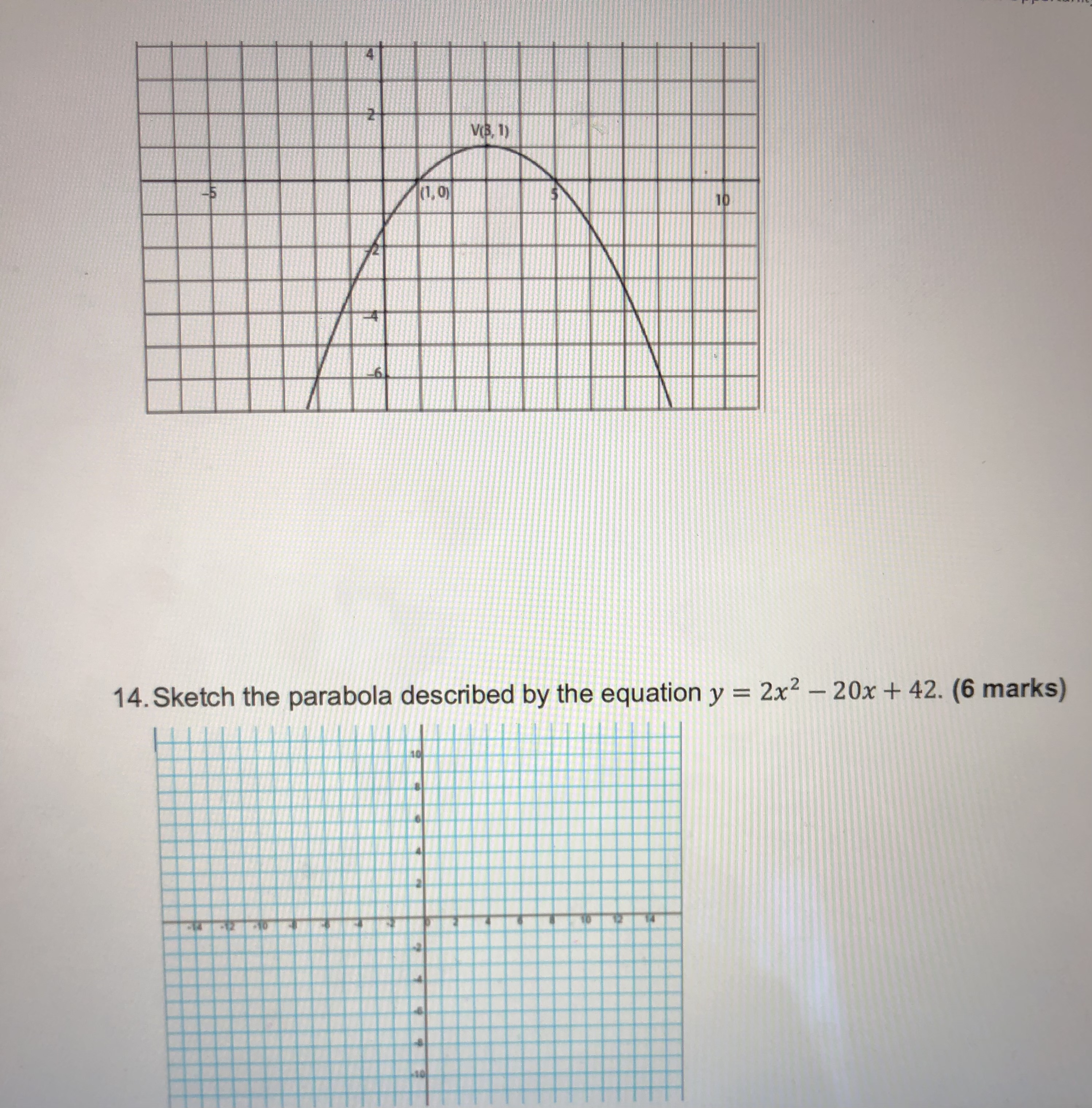
Task 1: Knowledge (25 marks) 1. Complete the following table: (10 marks) Equation in y = x2 y = -(x+5)2-3 y = 3x2 +4 vertex form a = h = k = Opens up or down? Compressed or stretched vertically? Vertex a minimum or maximum? Minimum or maximum value Equation of axis of symmetry Coordinates of vertex 2. Expand and simplify the following product, using the distributive property: (x - 3)(x + 2). (3 marks)3. Write the following equations in factored form. Remember to common factor first (if possible). a) y = 6x + 42 (2 marks) b) y = x2 - 6x - 27 (3 marks) c) y = 2x2 + 3x - 2 (4 marks) d) y = 16x2 - 9 (3 marks)4. Given the following graph of a parabola, find its equation, in the form y = a(x - h)2 + k (7 marks) VB. 1) 5. A parabola is defined by the equation y = x2 - 10x + 16. a) Write the equation in factored form. (2 marks) b) Identify the x-intercepts of the parabola. (2 marks) c) State the equation of the axis of symmetry. (1 mark)d) Determine the coordinates of the vertex. (2 marks) e) Sketch the parabola. (2 marks) 6. Write the following expression in vertex form by completing the square. (4 marks) y = x2-12x+7 7. A golf ball is hit from the top of a tee. The quadratic equation y = -5x2 + 20x + 0.05 describes its height, y, in metres as time, x, in seconds passes. Determine how long the ball is in the air. (5 marks)Hint: Use the quadratic formula. Task 3: Communication (25 marks) 8. Explain in detail the role of a, h, and k in the equation y = a(x - h)2 + k. You may use words, numerical examples, and sketches to support your explanation. (8 marks) 9. Think about the standard parabola defined by y = x2. How does the parabola defined by y = -4(x + 3)2 - 7 compare to the standard parabola? Describe all of the transformations. Then, draw a reasonable sketch of both parabolas. (6 marks)10. Factoring is an algebraic process, which is an essential one in the field of mathematics. Consider the following equation: y = x2 + 2x -8 This equation in factored form can be written as: y = (x - 2) (x + 4) Explain using words and algebra, how the zeros, the axis of symmetry, and the vertex can be obtained. (6 marks)11. Consider the graph of y = 2x: If the graph were extended much farther to the left from the interval shown, do you think the graph could ever touch or cross the x-axis? Explain in detail. (3 marks) Copyright @ 2022 The Ontario Educational Communications Authority. All rights reserved. TVO ILC MPM2D Learning Activity 4.5 I Assessment Opportunity 12. The graphs of y = 2* and y = x2 are shown here:Identify two major differences in behaviour between these graphs. (2 marks) 4= 2 2 Task 4: Thinking (25 marks) 13. For the following graph of the parabola, find its equation in the form y = a(x - h)2 + k. Then, express the answer in standard or expanded form, y = ax2 + bx + c. (9 marks)\f15. The amount of money that a local charity earns by selling T-shirts at a mall depends on the price of each T-shirt. The monthly profit, y, in dollars is given by the quadratic equation y = -35x2 + 1250x - 6500 where x represents the price of each T-shirt. a) Determine the roots of the equation. (3 marks) Copyright @ 2022 The Ontario Educational Communications Authority. All rights reserved. 8 TVO ILC MPM2D Learning Activity 4.5 Assessment Opportunity b) Determine the vertex of the parabola. (1 mark) c) Draw a sketch of the relationship. Label the axes and the vertex. (2 marks)d) Under what circumstances will the charity maximize its profit (make the most money)? (1 mark) e) Describe the significance of the roots in terms of the graph and in terms of the charity's venture. (1 mark) f) Determine the range of prices that the charity could consider, in order to make a monthly profit of at least $3000. (2 marks) cations Authority. All rights reserved. 9