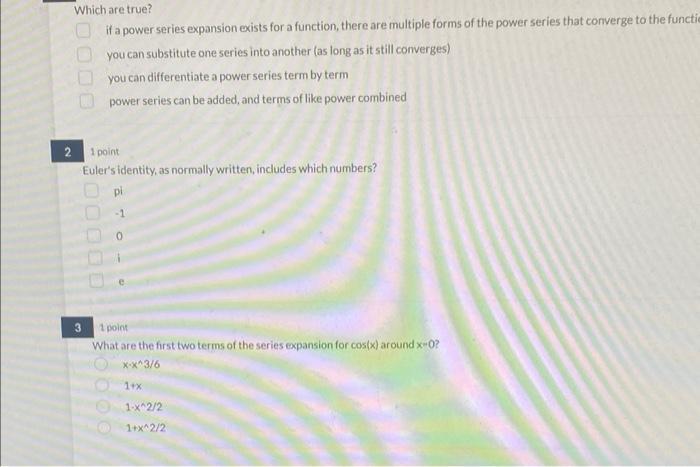
Which are true? if a power series expansion exists for a function, there are multiple forms of the power series that converge to the functie you can substitute one series into another (as long as it still converges) you can differentiate a power series term by term power series can be added, and terms of like power combined 1 point Euler's identity, as normally written, includes which numbers? 3 pi -1 1 point What are the first two terms of the series expansion for cos(x) around x-0? x-x^3/6 1+x 00 1-x^2/2 1+x^2/2