Telephone Touch-Tone

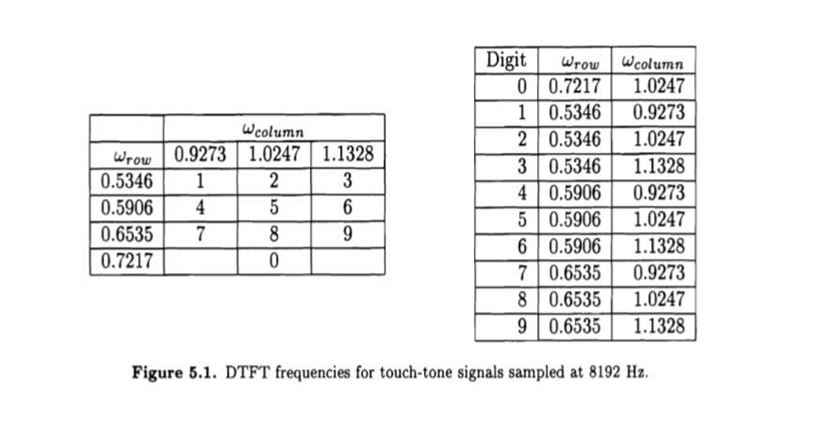
This exercise will teach you how the touch-tone system on the telephone uses signals of different frequencies to indicate which key has been pushed. The DTFT of a sampled telephone signal can be used to identify these frequencies. The sound you hear when you push a key is the sum of two sinusoids. The higher frequency sinusoid indicates the column of the key on the touch-pad and the lower frequency sinusoid indicates the row of the key on the touch-pad. Figure 5.1 shows the layout of a telephone keypad and the two DTFT frequencies corresponding to each digit, assuming the continuous-time waveform is sampled at 8192 kHz. The figure also contains a table listing each digit and the DTFT

frequencies for that digit. For example, the digit 5 is represented by the signal

d5[n] = sin(0.5906 n) + sin(1.0247 n)

Basic Problems

In these problems, you will create the appropriate touch-tone for each digit, and examine the DTFT to make sure the signals have the correct frequencies. You will also define a vector containing the touch-tones for your phone number.

(a). Create row vectors d0 through d9 to represent all 10 digits for the interval 0 ?n ? 999. Listen to each signal using sound. For example, sound(d2,8192) should sound like the tone you hear when you push a '2' on the telephone.

(b). The function fft can be used to compute N samples of the DTFT of a finite-length signal at frequencies wk = 2?k/N. For example, X = fft (x, 2048) computes 2048 evenly spaced samples of X(ejw) at wk = 2?k/2048 for 0 ? k ?2047. Use fft to compute samples of D2(ejw)

and D9(ejw) at wk = 2?k/2048. Define omega to be a vector containing wk, for 0 ? k ? 2047.

Plot the magnitudes of the DTFTs for these signals, and confirm that the peaks fall at the frequencies specified in Figure 5.1. You will find it easier to see which frequencies are present if you use axis to restrict the w-axis to the region 0.5 ? w ? 1.25 while keeping the full vertical range. Generate appropriately labeled plots of the DTFT magnitudes for these two digits.

(c). Define space to be a row vector with 100 samples of silence using zeros. Define phone to be your phone number by appending the appropriate signals and space. For instance, if your phone number was 555-7319, you would type

>> phone = [d5 space d5 space d5 space d7 space d3 space dl space d9] ;

Note that in order to append the signals this way, all of the digits you defined in Part (a) and space must be row vectors. Play your phone number using sound and verify that it sounds the same as when you dial it on a touch-tone phone.

Intermediate Problems

For these problems, you will learn to decode phone numbers from their touch-tones. The phone numbers to be decoded are in a file called touch.7z, which is uploaded to the Moodle. The data can be loaded into MATLAB by typing load x1 or load x2 as long as the file is in

your MATLABPATH. If the file loaded correctly, you should be able to list the names of variables by typing

>> who

Your variables are:

x1 x2

The vectors xl and x2 contain sampled versions of the sequence of touch-tones representing two different phone numbers. As in Part (c), the signals consist of 7 digits of 1000 samples each, separated by 100 samples of silence.

(d). Using fft, compute 2048 evenly spaced samples of the DTFT for each digit of x1. In order to apply fft to each digit separately, you will need to segment the signal into seven digits using the information you have about the relative lengths of the digits and spaces, or by plotting the signal and identifying when each digit starts and stops. Apply fftshift to the output of fft, which will rearrange the samples of the DTFT so they correspond to ascending frequencies in the range -?? wk ??. Define X11 through XI7 to contain these samples of the DTFT you obtained by applying fftshift to the output of fft for each digit. To determine the digits of the telephone number represented by xl, plot the magnitude of the DTFTs and compare the peak frequencies of the signals with those shown in Figure 5.1 As a check for your answer, the sum of the digits should be 41.

(e). Repeat Part (d) for tihe signal x2, and decode the digits of this phone number as well. These digits may not sum to 41.

Digit row wcolumn 0 0.7217 1.0247 1 0.5346 0.9273 column 21 0.5346 1.0247 wrou 0.9273 1.0247 1.1328 3 0.5346 1.1328 0.5346 1 2 3 4 0.5906 0.9273 0.5906 4 5 6 0.5906 1.0247 5 0.6535 7 8 9 6 0.5906 1.1328 7 0.6535 0.9273 8 0.6535 1.0247 9 0.6535 1.1328 Figure 5.1. DTFT frequencies for touch-tone signals sampled at 8192 Hz