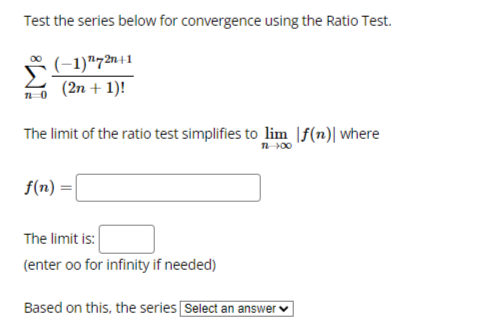
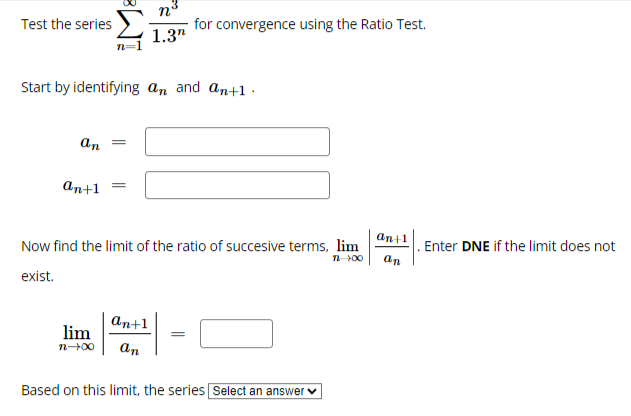
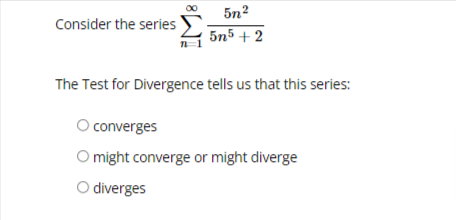
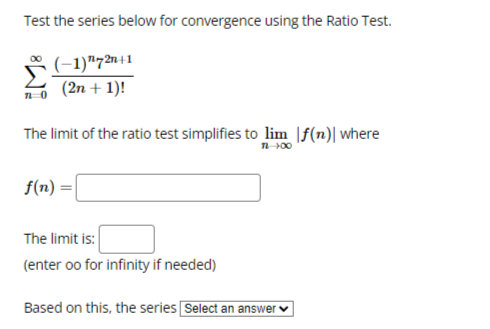
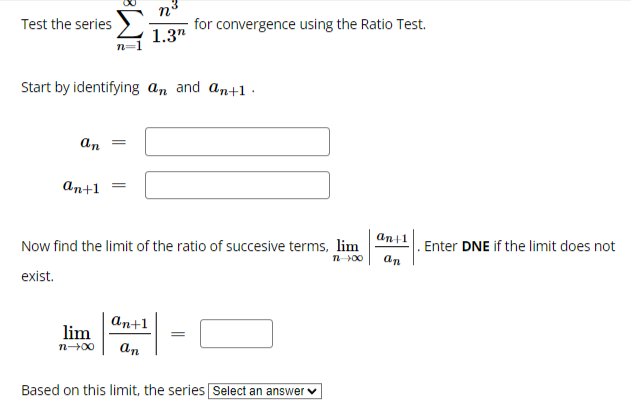
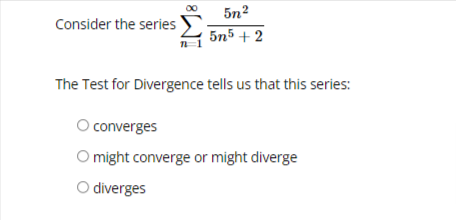
Test the series below for convergence using the Ratio Test. (-1)"72n41 (2n + 1)! The limit of the ratio test simplifies to lim If(n)| where n-+00 f(n) = The limit is: (enter oo for infinity if needed) Based on this, the series Select an answer vTest the series 1.3n for convergence using the Ratio Test. n=1 Start by identifying On and an+1 . an = an+1 Now find the limit of the ratio of succesive terms, lim Enter DNE if the limit does not 7 +00 an exist. an+1 lim n-+00 an Based on this limit, the series Select an answer v00 5n2 Consider the series 5n5 + 2 n 1 The Test for Divergence tells us that this series: O converges O might converge or might diverge O divergesgn Test the series for convergence using the Ratio Test. n! n 1 Start by identifying an and an+1 . an an+1 an|1 Now find the limit of the ratio of succesive terms, lim . Enter DNE if the limit does not 1-100 On exist. lim an+1 1-+00 an Based on this limit, the series Select an answer v