thats all the prof gave. maybe u can use this as reference

its proving not finding

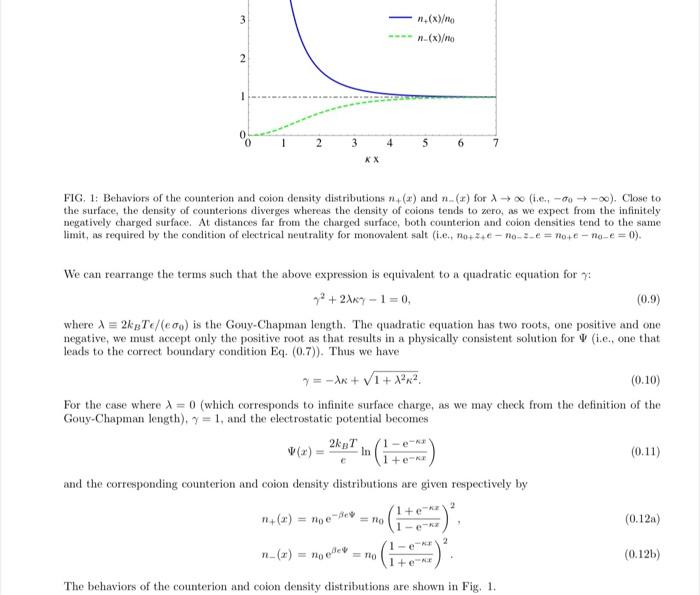
Problem 2: Poisson-Boltzmann equation for divalent counterions (10 points) The Poisson-Boltzmann equation (PBE) is a nonlinear differential equation, which yields analytic solutions only for certain ionic valences. In general, for ions of arbitrary valences, a useful approximation is the Debye-Hckel approximation to the Poisson-Boltzmann equation, which is valid if the salt concentration is sufficiently small (and the electrostatic potential is weak enough). On the other hand, an analytic solution does exist for the case of a salt solution consisting of divalent counterions and monovalent coions, in the presence of a negatively charged, flat surface. Let's check that this is indeed the case. We start with the PBE for arbitrary ionic valences, which is given by av = 2+e note -B2+eV The charge neutrality of salt ions is expressed by 2+eno+ - 2-eno, = 0 Using this equation, and defining a rescaled potential O = Bey and a rescaled distance X= kx, where is the Debye length, we can express the PBE in the dimensionless form ? 1 X2 (ez-P-e-+P) 2+ + 2 .c 2_en_ez_ev a. For the case of divalent counterions and monovalent coions, check that a solution to the equation above is given by 1+ 4e - te-2x (X) = In (1 - e-X)2 [4 points] b. Plot the rescaled distribution of counterions, n-o+ = exp(-z-0), and the rescaled distribution of coions, n-Ino+ = (no- Ino+)exp(z_0), as functions of X. [6 points) Problem 1. Single charged surface in monovalent salt solution The Poisson-Boltzmann equation (PBE) is given by av 3r Roces (0.1) - nocer We are asked to show that 2T 1-9 2kpT In (In(1 - **) - In(1 + 70 ) 1+ eK (0.2) is a solution to the above PBE. So we have to substitute this expression for V into both sides of the PBE, and show that they agree with each other. We start with the left-hand side (LHS) of the PBE, differentiating twice with respect to r: 4k Txoek (0.3a) Or e(1-12e-2)' 2v 4k 7k (1 + y2e-2xt)ex r2 e(1-12e-2x)2 (0.3) The inverse square Debye length is given by (no+ +10-22)e201002 kg kgT' (0.4) whereupon we obtain 1 + 12e-22 =Snoeye 3.2 (1-12e-2x) (0.5) On the right-hand side (RHS) of the PBE, we have ->) -(17) noe (0.6) 1+ yek 1-9e- 1+ ye 87c-**(1 + 80-28) (1-72e-222 We compare the LHS (i.c., Eq. (0.5)) with the RHS (i.e, Eq. (0.6)), and note that they are equal. To determine the value of we apply the boundary condition at the charged surface, viz., a 3. Using Eq. (0.3a), we obtain 4kpTky c(1-12) 0 (0.7) do (0.8) 3 6.(x)/10 .(x)o 2 2 3 4 5 6 7 KX FIG. 1: Behaviors of the counterion and colon density distributions +(a) and ...(x) for ^ (e- 0-0). Close to the surface, the density of counterions diverges whereas the density of coions tends to zero, as we expect from the infinitely negatively charged surface. At distances far from the charged surface, both counterion and coion densities tend to the same limit, as required by the condition of electrical neutrality for monovalent salt (.e., 90+244-no-ze=10+ -no-e = 0). We can rearrange the terms such that the above expression is equivalent to a quadratic equation for 72 +27 - 1=0, (0.9) where I = 2kgTe/(eco) is the Gouy-Chapman length. The quadratic equation has two roots, one positive and one negative, we must accept only the positive root as that results in a physically consistent solution for (i.e., one that leads to the correct boundary condition Eq. (0.7)). Thus we have y = -x + 1 + 12x2 (0.10) For the case where I = 0 (which corresponds to infinite surface charge, as we may check from the definition of the Gouy-Chapman length), 9 = 1, and the electrostatic potential becomes 2kpT in (0.11) 1+eK and the corresponding counterion and coion density distributions are given respectively by 1 + e 1 -- (0.12) n_() = node STO (0.125) 1+ The behaviors of the counterion and coion density distributions are shown in Fig. 1. Problem 2: Poisson-Boltzmann equation for divalent counterions (10 points) The Poisson-Boltzmann equation (PBE) is a nonlinear differential equation, which yields analytic solutions only for certain ionic valences. In general, for ions of arbitrary valences, a useful approximation is the Debye-Hckel approximation to the Poisson-Boltzmann equation, which is valid if the salt concentration is sufficiently small (and the electrostatic potential is weak enough). On the other hand, an analytic solution does exist for the case of a salt solution consisting of divalent counterions and monovalent coions, in the presence of a negatively charged, flat surface. Let's check that this is indeed the case. We start with the PBE for arbitrary ionic valences, which is given by av = 2+e note -B2+eV The charge neutrality of salt ions is expressed by 2+eno+ - 2-eno, = 0 Using this equation, and defining a rescaled potential O = Bey and a rescaled distance X= kx, where is the Debye length, we can express the PBE in the dimensionless form ? 1 X2 (ez-P-e-+P) 2+ + 2 .c 2_en_ez_ev a. For the case of divalent counterions and monovalent coions, check that a solution to the equation above is given by 1+ 4e - te-2x (X) = In (1 - e-X)2 [4 points] b. Plot the rescaled distribution of counterions, n-o+ = exp(-z-0), and the rescaled distribution of coions, n-Ino+ = (no- Ino+)exp(z_0), as functions of X. [6 points) Problem 1. Single charged surface in monovalent salt solution The Poisson-Boltzmann equation (PBE) is given by av 3r Roces (0.1) - nocer We are asked to show that 2T 1-9 2kpT In (In(1 - **) - In(1 + 70 ) 1+ eK (0.2) is a solution to the above PBE. So we have to substitute this expression for V into both sides of the PBE, and show that they agree with each other. We start with the left-hand side (LHS) of the PBE, differentiating twice with respect to r: 4k Txoek (0.3a) Or e(1-12e-2)' 2v 4k 7k (1 + y2e-2xt)ex r2 e(1-12e-2x)2 (0.3) The inverse square Debye length is given by (no+ +10-22)e201002 kg kgT' (0.4) whereupon we obtain 1 + 12e-22 =Snoeye 3.2 (1-12e-2x) (0.5) On the right-hand side (RHS) of the PBE, we have ->) -(17) noe (0.6) 1+ yek 1-9e- 1+ ye 87c-**(1 + 80-28) (1-72e-222 We compare the LHS (i.c., Eq. (0.5)) with the RHS (i.e, Eq. (0.6)), and note that they are equal. To determine the value of we apply the boundary condition at the charged surface, viz., a 3. Using Eq. (0.3a), we obtain 4kpTky c(1-12) 0 (0.7) do (0.8) 3 6.(x)/10 .(x)o 2 2 3 4 5 6 7 KX FIG. 1: Behaviors of the counterion and colon density distributions +(a) and ...(x) for ^ (e- 0-0). Close to the surface, the density of counterions diverges whereas the density of coions tends to zero, as we expect from the infinitely negatively charged surface. At distances far from the charged surface, both counterion and coion densities tend to the same limit, as required by the condition of electrical neutrality for monovalent salt (.e., 90+244-no-ze=10+ -no-e = 0). We can rearrange the terms such that the above expression is equivalent to a quadratic equation for 72 +27 - 1=0, (0.9) where I = 2kgTe/(eco) is the Gouy-Chapman length. The quadratic equation has two roots, one positive and one negative, we must accept only the positive root as that results in a physically consistent solution for (i.e., one that leads to the correct boundary condition Eq. (0.7)). Thus we have y = -x + 1 + 12x2 (0.10) For the case where I = 0 (which corresponds to infinite surface charge, as we may check from the definition of the Gouy-Chapman length), 9 = 1, and the electrostatic potential becomes 2kpT in (0.11) 1+eK and the corresponding counterion and coion density distributions are given respectively by 1 + e 1 -- (0.12) n_() = node STO (0.125) 1+ The behaviors of the counterion and coion density distributions are shown in Fig. 1