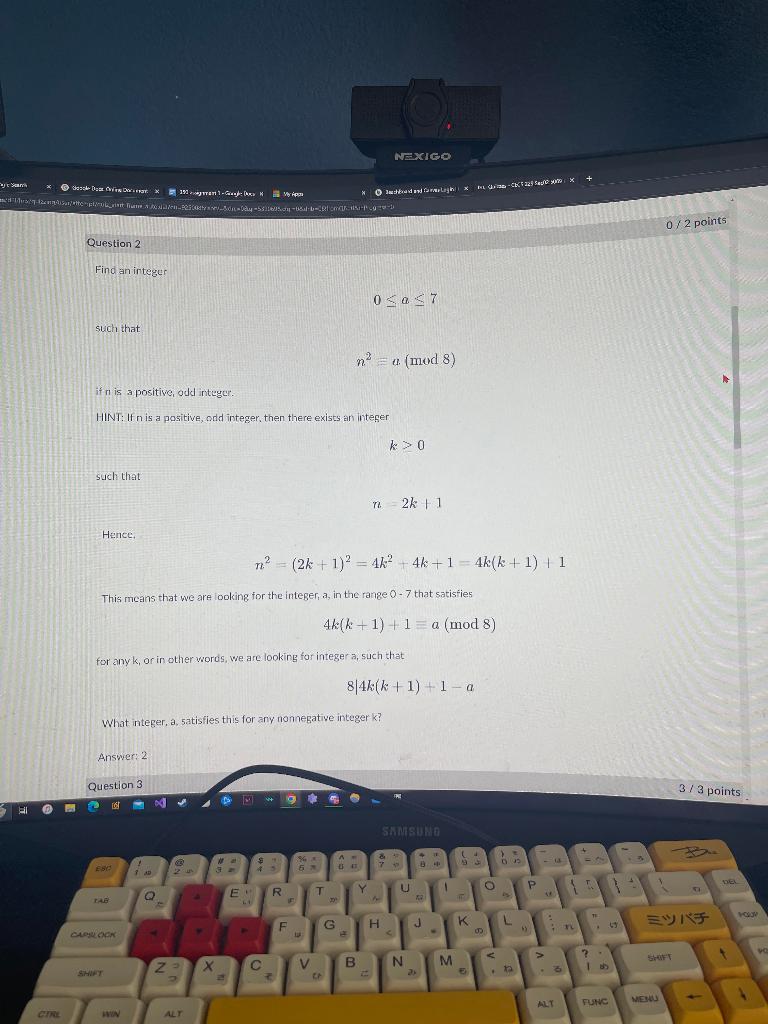
The answer is not "2"

Find an integer 0a7 such that n2=u(mod8) if n is a positive, odd integer. HINT: If n is a positive, odd integer, then there exists an integer k>0 such that n=2k+1 Hence, n2=(2k+1)2=4k2+4k+1=4k(k+1)+1 This means that we are looking for the integer, a, in the range 07 that satisfies 4k(k+1)+1a(mod8) for any k, or in other words, we are looking for integer a, such that 84k(k+1)+1a What integer, a, 5atisfies this for any nonnegative integer k