The answer is provided, but I did not understand it, please, explain it in a way I am able to understand the answer, do not just recopy it, thank you!

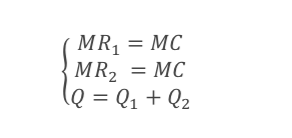
* During the Iran-Iraq war, the same arms merchant often sold weapons to both sides of the conflict. In this situation, a different price could be offered to each side because there was little danger that the country offered the lower price would sell arms to its rival to profit on the difference in prices. Suppose a French arms merchant has a monopoly of Exocet air-to-sea missiles and is willing to sell them to both sides. Iraq's demand for Exocets is P1 = 400 - 0.50, and Iran's is P2 = 300 Q2, where P is in millions of euros. The marginal cost of Exocets is MC = Q, where Q = Q1 + Q2. What price will be charged to each country? ANSWER: P1 = 400 - 0.501 => MR1 = 400 - Q1, or Q1 = 400 - MR1. P2 = 300 - Q2 => MR2 = 300 - 202, or Q2 = 150 - MRz. The firm is optimizing when MR1 = MR2 = MC. Note that this also implies that marginal revenue from producing in both markets, MR, should be also equal to MC. To get "total" MR we need to add MR, and MR2 horizontally (this means adding quantities). See the graph below. Note that when MR is greater than 300 the merchant sells missiles only in the first market, so total MR curve consists of two pieces: 400 - MR, 0 100 (see graph). 3 In equilibrium, MR=MC or - - 20 = Q, which solves for Q=220 and MR=220. Q1 = 400 - MR1 = 180; P1 = 400 - 0.5Q1 = 310. Q2 = 150 - MR2 = 40; 2 P2 = 300 - Q2 = 260. P P2 MR. MC 100 310 300 300 MC 260 220 D1 MR MR1 MR2 \\D2 180 Q1 40 Q2 100 220 Q Note that you will get the same results by solving the system of equations:MR = MC MR MC 2 2 = Q1+ Q2