The attached file contains hypothetical data for working this problem. Goodman Corporations and Landry Incorporateds stock prices and dividends, along with the Market Index, are shown in the file. Stock prices are reported for December 31 of each year, and dividends reflect those paid during the year. The market data are adjusted to include dividends.

1. Use the data given to calculate annual returns for Goodman, Landry, and the Market Index, and then calculate average returns over the five-year period. (Hint: Remember, returns are calculated by subtracting the beginning price from the ending price to get the capital gain or loss, adding the dividend to the capital gain or loss, and dividing the result by the beginning price. Assume that dividends are already included in the index. Also, you cannot calculate the rate of return for 2015 because you do not have 2014 data.)
2. Calculate the standard deviation of the returns for Goodman, Landry, and the Market Index. (Hint: Use the sample standard deviation formula given in the chapter, which corresponds to the STDEV function in Excel.)
3. On a stand-alone basis which corporation is the least risky?
4. Construct a scatter diagram graph that shows Goodmans and Landry returns on the vertical axis and the Market Indexs returns on the horizontal axis.
5. Estimate Goodmans and Landrys betas as the slopes of regression lines with stock returns on the vertical axis (y-axis) and market return on the horizontal axis (x-axis). (Hint: use Excels SLOPE function.) Are these betas consistent with your graph?
6. The risk-free rate on long-term Treasury bonds is 8.04%. Assume that the market risk premium is 6%. What is the expected return on the market? Now use the SML equation to calculate the two companies' required returns.
7. If you formed a portfolio that consisted of 60% Goodman stock and 40% Landry stock, what would be its beta and its required return?
8. Suppose an investor wants to include Goodman Industries stock in his or her portfolio. Stocks A, B, and C are currently in the portfolio, and their betas are 0.769, 0.985, and 1.423, respectively. Calculate the new portfolios required return if it consists of 30% of Goodman, 20% of Stock A, 30% of Stock B, and 20% of Stock C.

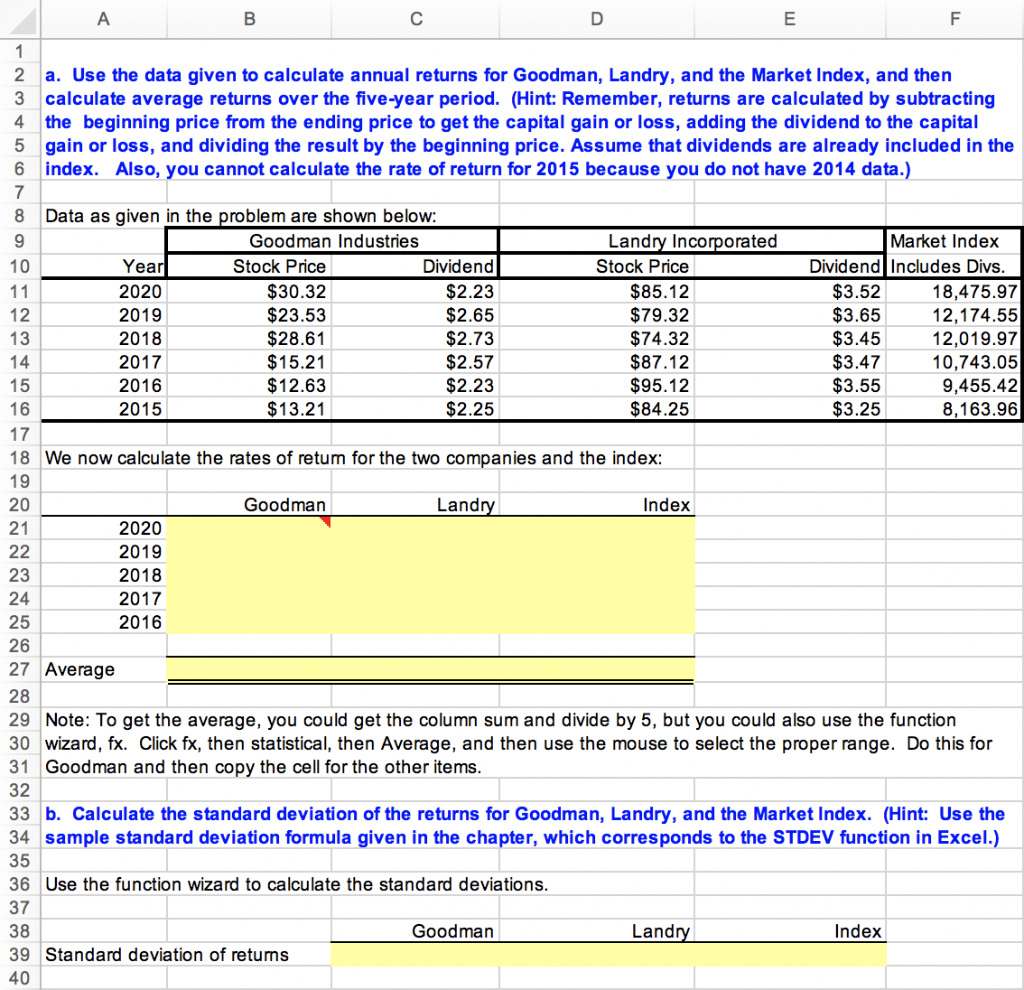
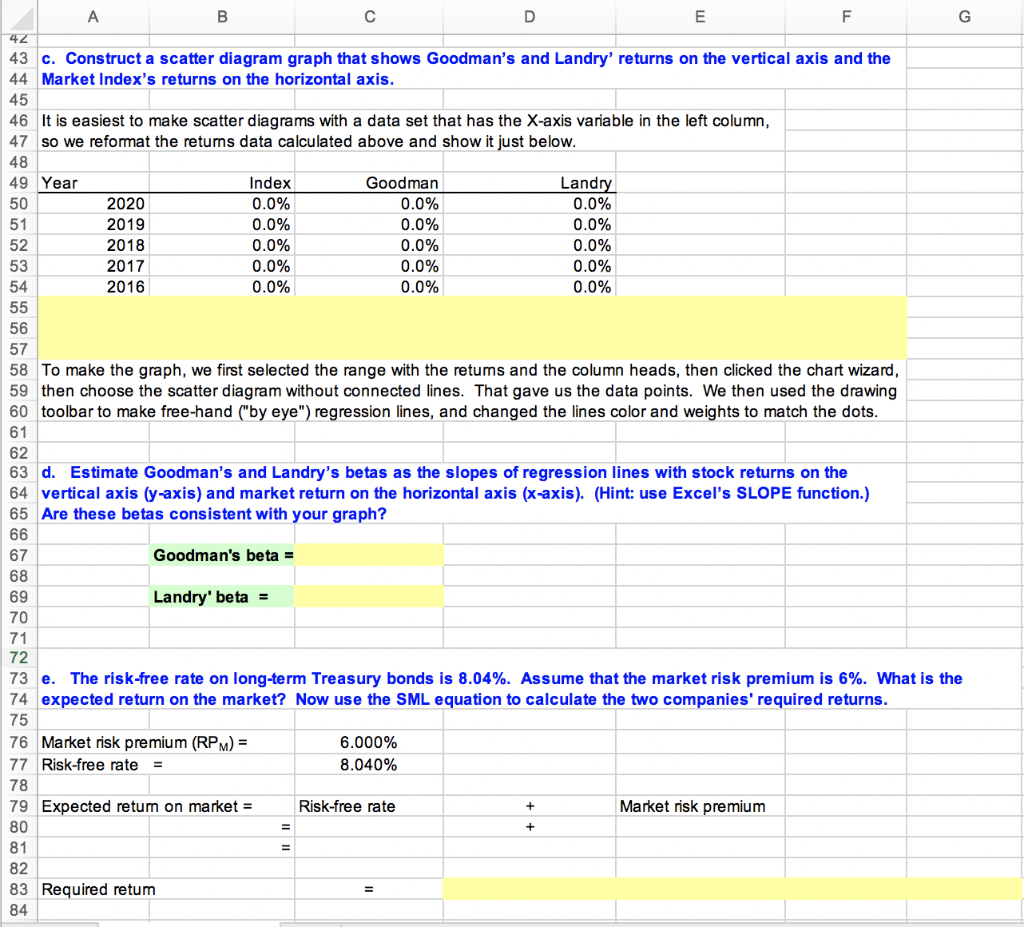
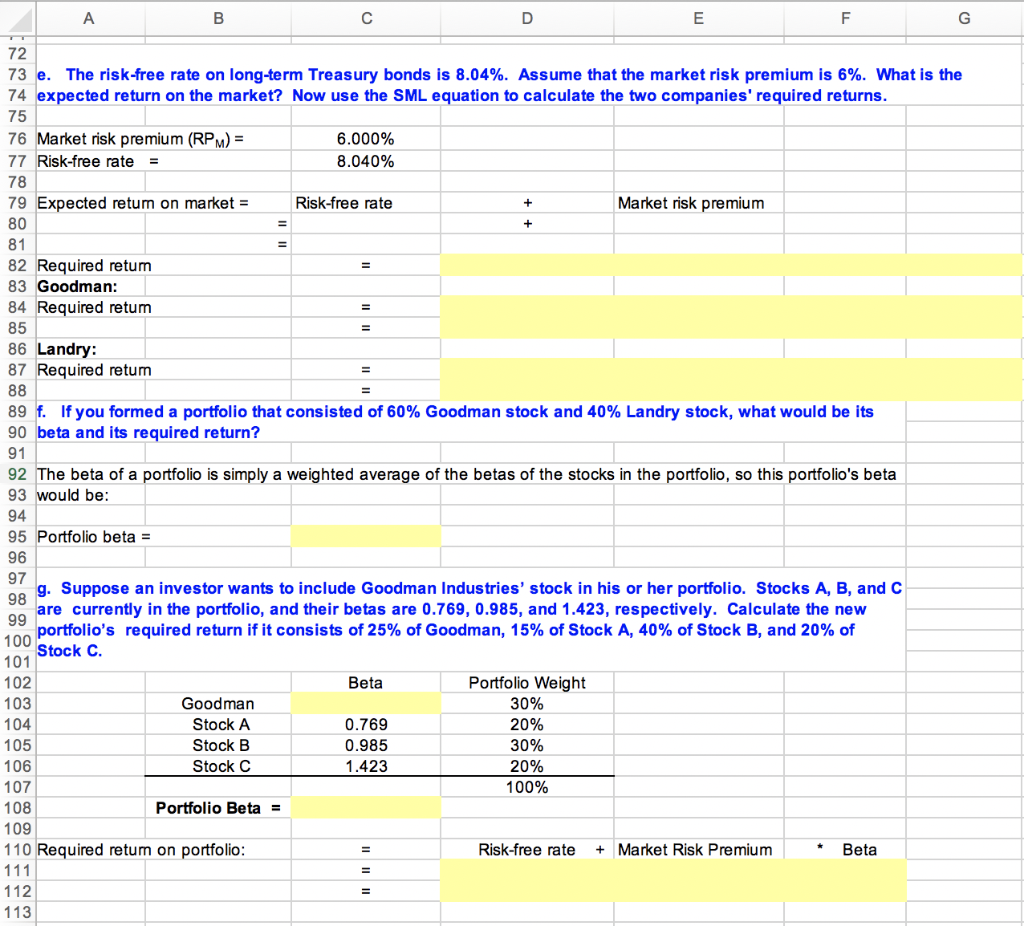
A B D E F 1 2 a. Use the data given to calculate annual returns for Goodman, Landry, and the Market Index, and then 3 calculate average returns over the five-year period. (Hint: Remember, returns are calculated by subtracting 4 the beginning price from the ending price to get the capital gain or loss, adding the dividend to the capital 5 gain or loss, and dividing the result by the beginning price. Assume that dividends are already included in the 6 index. Also, you cannot calculate the rate of return for 2015 because you do not have 2014 data.) 7 8 Data as given in the problem are shown below: 9 Goodman Industries Landry Incorporated Market Index 10 Year Stock Price Dividend Stock Price Dividend Includes Divs. 11 2020 $30.32 $2.23 $85.12 $3.52 18,475.97 12 2019 $23.53 $2.65 $79.32 $3.65 12,174.55 13 2018 $28.61 $2.73 $74.32 $3.45 12,019.97 14 2017 $15.21 $2.57 $87.12 $3.47 10,743.05 15 2016 $12.63 $2.23 $95.12 $3.55 9,455.42 16 2015 $13.21 $2.25 $84.25 $3.25 8,163.96 17 18 We now calculate the rates of return for the two companies and the index: 19 20 Goodman Landry Index 21 2020 22 2019 23 2018 24 2017 25 2016 26 27 Average 28 29 Note: To get the average, you could get the column sum and divide by 5, but you could also use the function 30 wizard, fx. Click fx, then statistical, then Average, and then use the mouse to select the proper range. Do this for 31 Goodman and then copy the cell for the other items. 32 33 b. Calculate the standard deviation of the returns for Goodman, Landry, and the Market Index. (Hint: Use the 34 sample standard deviation formula given in the chapter, which corresponds to the STDEV function in Excel.) 35 36 Use the function wizard to calculate the standard deviations. 37 38 Goodman Landry Index 39 Standard deviation of returns 40 B D F G 42 43 c. Construct a scatter diagram graph that shows Goodman's and Landry' returns on the vertical axis and the 44 Market Index's returns on the horizontal axis. 45 46 It is easiest to make scatter diagrams with a data set that has the X-axis variable in the left column, 47 so we reformat the returns data calculated above and show it just below. 48 49 Year Index Goodman Landry 50 2020 0.0% 0.0% 0.0% 51 2019 0.0% 0.0% 0.0% 52 2018 0.0% 0.0% 0.0% 53 2017 0.0% 0.0% 0.0% 54 2016 0.0% 0.0% 0.0% 55 56 57 58 To make the graph, we first selected the range with the returns and the column heads, then clicked the chart wizard, 59 then choose the scatter diagram without connected lines. That gave us the data points. We then used the drawing 60 toolbar to make free-hand ("by eye") regression lines, and changed the lines color and weights to match the dots. 61 62 63 d. Estimate Goodman's and Landry's betas as the slopes of regression lines with stock returns on the 64 vertical axis (y-axis) and market return on the horizontal axis (x-axis). (Hint: use Excel's SLOPE function.) 65 Are these betas consistent with your graph? 66 67 Goodman's beta = 68 69 Landry' beta = 70 71 72 73 e. The risk-free rate on long-term Treasury bonds is 8.04%. Assume that the market risk premium is 6%. What is the 74 expected return on the market? Now use the SML equation to calculate the two companies' required returns. 75 76 Market risk premium (RPM) = 6.000% 77 Risk-free rate = 8.040% 78 79 Expected return on market = Risk-free rate Market risk premium 80 81 82 83 Required retum 84 + + B D E F G + + = 72 73 e. The risk-free rate on long-term Treasury bonds is 8.04%. Assume that the market risk premium is 6%. What is the 74 expected return on the market? Now use the SML equation to calculate the two companies' required returns. 75 76 Market risk premium (RPM) = 6.000% 77 Risk-free rate = 8.040% 78 79 Expected retum on market = Risk-free rate Market risk premium 80 81 82 Required retum 83 Goodman: 84 Required retum 85 86 Landry: 87 Required retum 88 89 f. If you formed a portfolio that consisted of 60% Goodman stock and 40% Landry stock, what would be its 90 beta and its required return? 91 92 The beta of a portfolio is simply a weighted average of the betas of the stocks in the portfolio, so this portfolio's beta 93 would be: 94 95 Portfolio beta = 96 97 g. Suppose an investor wants to include Goodman Industries' stock in his or her portfolio. Stocks A, B, and C 98 are currently in the portfolio, and their betas are 0.769, 0.985, and 1.423, respectively. Calculate the new 99 portfolio's required return if it consists of 25% of Goodman, 15% of Stock A, 40% of Stock B, and 20% of 100 Stock C. 101 102 Beta Portfolio Weight 103 Goodman 30% 104 Stock A 0.769 20% 105 Stock B 0.985 30% 106 Stock C 1.423 20% 107 100% 108 Portfolio Beta = 109 110 Required retum on portfolio: Risk-free rate Market Risk Premium Beta 111 112 113 + =