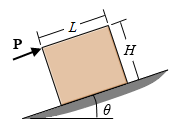
The block shown in $($Figure $1)$ has a mass of mm $=50$ kgkg $,$ a height HH $=1\mathrm{.}3$ mm $,$ and width LL $=2$ mm $.$ It is resting on a ramp that makes an angle $=39$ with the horizontal. A force PP is applied parallel to the surface of the ramp at the top of the block. What is the maximum force that can be applied without causing the block to move? The coefficient of static friction is ss $=0\mathrm{.}45,$ and the center of mass of the block is at the center of the rectangle.

Figure

$2$ of $2$

Part A

Part complete

There are two ways the block can move: by slipping up the ramp or by tipping over. First consider the block slipping up the ramp. What is the magnitude of the normal force between the block and the ramp?

Express your answer to three significant figures with appropriate units.

View Available Hint$($s$)$for Part A

NN $=$

$381$ NN

SubmitPrevious$$Answers

Correct

Correct answer is shown. Your answer $380$N$380$N was either rounded differently or used a different number of significant figures than required for this part.

Part B

Part complete

What is the maximum magnitude of PP that can be applied before slipping would occur, assuming the block does not tip?

Express your answer to three significant figures with appropriate units.

View Available Hint$($s$)$for Part B

PslipPslip $=$

$480$ NN

SubmitPrevious$$Answers

Correct

Correct answer is shown. Your answer $479\mathrm{.}814$N$479\mathrm{.}814$N was either rounded differently or used a different number of significant figures than required for this part.

Part C

Part complete

Now consider the case of impending tipping. Where do the normal force and friction force act in this case?

At the point directly below the center of gravity of the block.At the edge of the block closest to the bottom of the ramp.At the edge of the block closest to the top of the ramp.At an unknown point along the bottom edge of the block.At the midpoint of the bottom edge of the block.

SubmitPrevious$$Answers

Correct

Part D

Part complete

Use the free$-$body diagram shown in $($Figure $2)$ and choose the correct equilibrium equation for the moments about the point of contact.

$$MO$=0=$WLcos$($$)/2$WHsin$($$)/2$MO$=0=$WLcos$($$)/2$WHsin$($$)/2$MO$=0=$PH$$WLsin$($$)/2$WHcos$($$)/2$MO$=0=$PH$$WLsin$($$)/2$WHcos$($$)/2$MO$=0=$PH$+$WLsin$($$)/2+$WHcos$($$)/2$MO$=0=$PH$+$WLsin$($$)/2+$WHcos$($$)/2$MO$=0=$PH$+$WHsin$($$)/2$MO$=0=$PH$+$WHsin$($$)/2$MO$=0=$PH$+$WLcos$($$)/2$MO$=0=$PH$+$WLcos$($$)/2$MO$=0=$PH$+$WLcos$($$)/2+$WHsin$($$)/2$MO$=0=$PH$+$WLcos$($$)/2+$WHsin$($$)/2$

SubmitPrevious$$Answers

Correct

Part E

What is the maximum magnitude of PP that can be applied before tipping would occur, assuming the block does not slip?

Express your answer to three significant figures with appropriate units.

Activate to select the appropriates template from the following choices. Operate up and down arrow for selection and press enter to choose the input value typeActivate to select the appropriates symbol from the following choices. Operate up and down arrow for selection and press enter to choose the input value type

PtipPtip $=$

$427\mathrm{.}50$N

SubmitPrevious$$AnswersRequest$$Answer

Incorrect; Try Again; $5$ attempts remaining

Check your trigonometry.

Part F

What is the maximum magnitude of PP that does not cause motion of the block?

Express your answer to three significant figures with appropriate units.