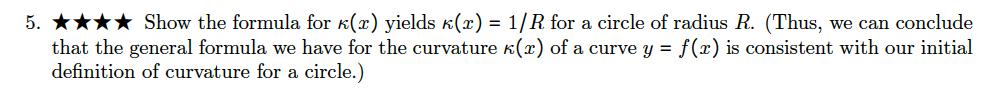
The circle will form the basis for our thinking about curvature; we want its curvature to be the same at every point on the circle. Let us define the curvature at any point on a circle to be = 1/R, where R is the radius of the circle. Note the smaller the radius of the circle, the larger its curvature, and the larger the radius of the circle, the smaller its curvature. Since we intend to define curvature for more general curves by studying the way the curve deviates from its tangent line at any point, we expect the curvature of a straight line to be 0. For now, let us define the curvature of a straight line to be 0. P Figure 1: The symmetry of a circle means the circle deviates from its tangent line at point P in the same way as at point P' for any pair of points P and P'. Consider now curves that are the graphs of functions y = f(x), where f(x) is a twice-differentiable function both f'(x) and f"(x) exist. We can consider such curves to be smooth in the sense there is a tangent line at every point on the curve, and the concavity is also defined at every point. Since we suppose f"(2) exists everywhere, we are able to use it to study the way the slopes of tangent lines change nearby any point on the curve - if f"(x) is large at any point, then the slopes of tangent lines undergo a large change as we move through that point. This means the graph of the function near such a point has a very sharp turn in it. We will define the curvature of a curve given by y = f(x) to be K(x) = |f"(x)| (1+ (f'(x)))/2 Now that we have a value for the curvature of a function at a given point, we can define the radius of curvature at that point to be 1 p(x) = K(x)' whenever (x) # 0. We can associate to p(x) a circle of this radius tangent to the curve y = f(x) at the point (x, y). This circle is the circle that best approximates the curvature of the curve at this point, and the graph of the function and this circle have the same tangent line at this point. This circle is called the osculating circle. 5. Show the formula for (x) yields (x) = 1/R for a circle of radius R. (Thus, we can conclude that the general formula we have for the curvature (x) of a curve y = f(x) is consistent with our initial definition of curvature for a circle.)