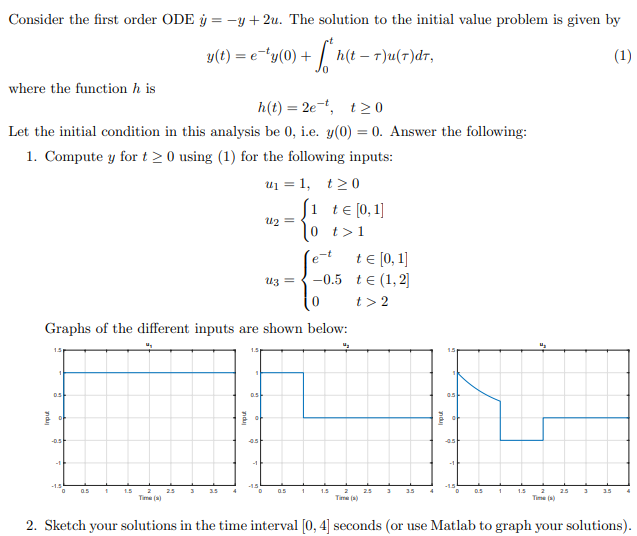
The closed-form solution to a general IVP for a first order linear ODE will be used to compute the dependent variable for a handful of inputs. The main point is to get comfortable with the convolution representation of the zero-state response. A quick sketch of h(tr) and u(7) as a function of 7 for various t's is quite useful in sorting out how to compute the integral. Consider the first order ODE = y+2u. The solution to the initial value problem is given by where the function h is y(t) = ey(0) + [ h(t t)u(7)dr, 0 - h(t)=2et, t0 Let the initial condition in this analysis be 0, i.e. y(0) = 0. Answer the following: 1. Compute y for t 0 using (1) for the following inputs: u = 1, t0 (1) 1 t [0,1] U2 = 0 t>1 t = [0,1] uz = -0.5 t = (1,2] Graphs of the different inputs are shown below: t>2 Input 1 05 -0.5 -1 andup -h du 05 -1.5 -15 -15 0 05 1 1.5 2 25 3 35 4 0.5 1 1.5 2 25 3 3.5 4 D 0.5 1 15 2 25 3 35 Time() Time(s) Time(s) 2. Sketch your solutions in the time interval [0,4] seconds (or use Matlab to graph your solutions).