Question: The code is in MATLAB Equilibrium occurs when there is no motion in a particle. Mathematically, this is represented when all the forces acting on
The code is in MATLAB
Equilibrium occurs when there is no motion in a particle. Mathematically, this is represented when all the forces acting on an object in all direction sum to 0.
F = F1 + F2 + F3 + [ ] = 0
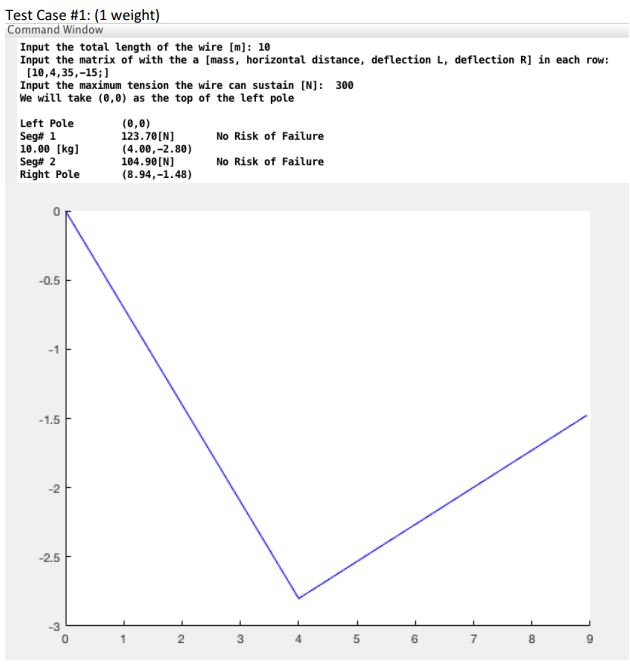
You are provided a massless un-stretchable rope of length L [m] between two poles. A series of weights have been placed on the rope and caused the rope to deflect. The only information you have about the weights are their masses M [kg], their horizontal distance from the left pole D [m] and the deflection of the rope to the left and the right of the point from the negative and positive x-axis respectively taking clockwise to be positive A [degrees].
Note: The rope applies a tension force in the direction of the deflection at each mass.
The goal of this part is to determine the tension of the rope. You will need to sum forces at each point and determine the force of tension in each segment of the rope. If any segment of rope sustains more than a certain amount of tension, there is the possibility of it breaking. Different types of material rope can withstand a specified maximum tension. Use a menu to allow the user to select a material with tension (menu). Inform the user which segments of rope fail under this risk if the tension of the rope exceeds the maximum tension allowed for the material selected. You will need to research different material. The test case provided in the supporting document is based on a rope that can withstand 100 N tension force. Your code should relate to the specific material.

The result of your code should plot the deflection of the rope with the weights and identify the segments that would be under too much tension by making that segment red. Assumptions that must be validations
No angle should exceed 90 degrees. NOTE: this would mean that the wire is going the wrong direction.
Weights should be positive
The deflection left should be the same as the deflection right of the previous weight.
The length of the rope and the length of rope calculated using the horizontal distance and angles should be within a small margin of error to account for rounding.
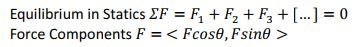
![+ F2 + F3 + [ ] = 0 You are provided](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f4eb803672f_10366f4eb7facfe8.jpg)
![a massless un-stretchable rope of length L [m] between two poles. A](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f4eb8108029_10466f4eb80641ec.jpg)
Table 1: Sample Test Case Mass (kg) 9 1.72578 9 Horizontal Distance Deflection Left .5 1 1.5 Deflection Right 45 5 -5 -5 -45 Table 1: Sample Test Case Mass (kg) 9 1.72578 9 Horizontal Distance Deflection Left .5 1 1.5 Deflection Right 45 5 -5 -5 -45
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


