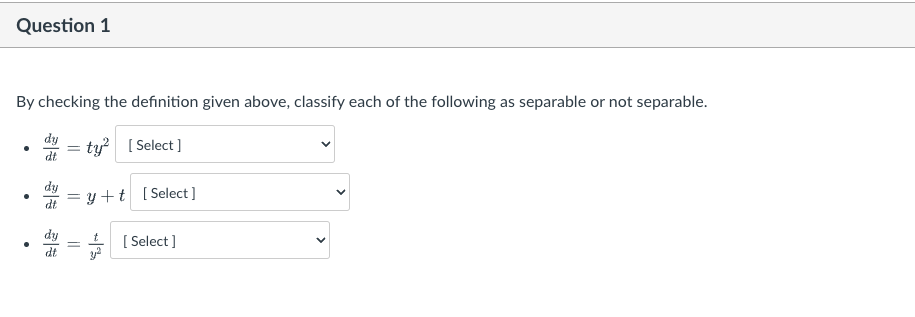
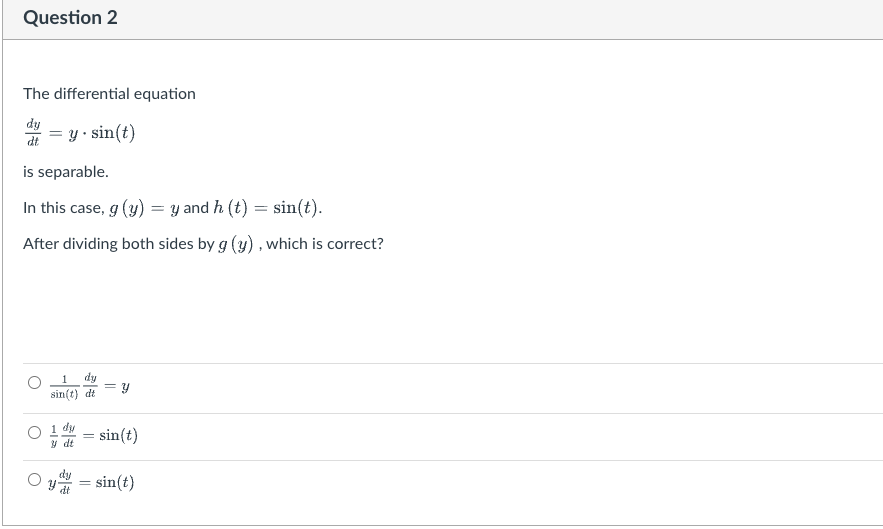
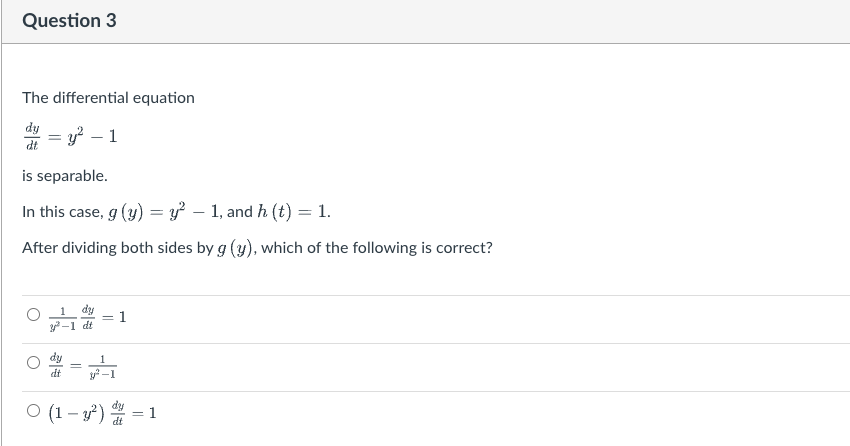
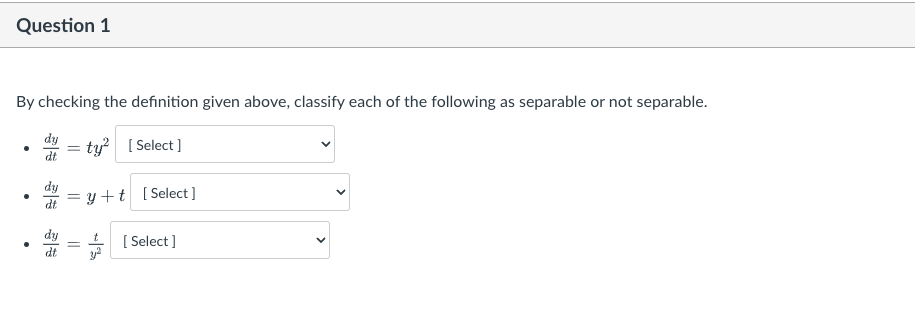
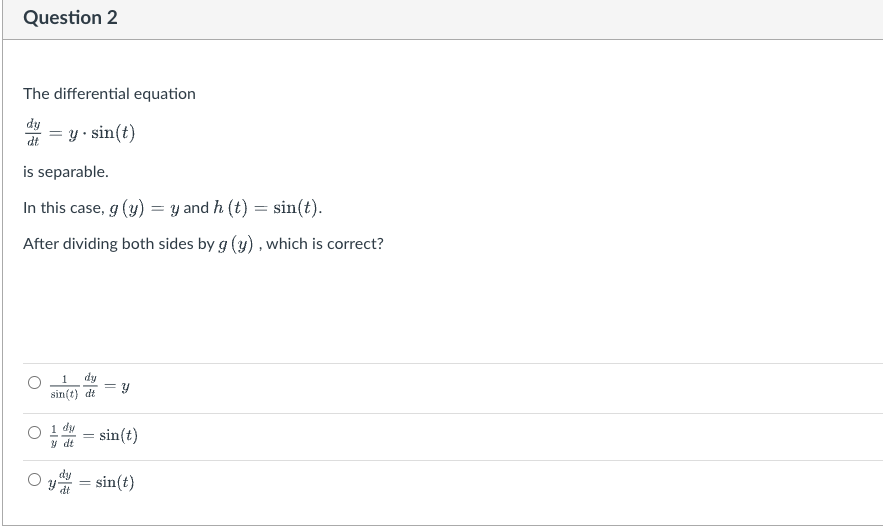
The definition of a separable differential equation A separable differential equation is one that can be written in the form at = g(y) . h (t). When we work on solving the separable differential equation, we divide both sides by g (y). Then the equation has this format: dy gly) de = h (t). Note: every autonomous first order differential equation is separable, with h (t) = 1.Question 1 By checking the definition given above, classify each of the following as separable or not separable. dy [ Select ] dt = ty- dy = y+t [ Select ] v dt dy [ Select ] V dtQuestion 2 The differential equation is separable. In this case, 9 (y) : y and h (t) : sint). After dividing both sides by g {3;} ,which is correct? Question 3 The differential equation is separable. In this case, 9 [y] = 3:2 Land h (t) = 1. After dividing both sides by g (3;), which of the following is correct? 1 d3: _ 0 ET 1 dsr 1 O 3 1151