Question: The event tree, shown below, analyses a failsafe mechanism consisting of three (3) components. In the event of a fault, . Component A should operate

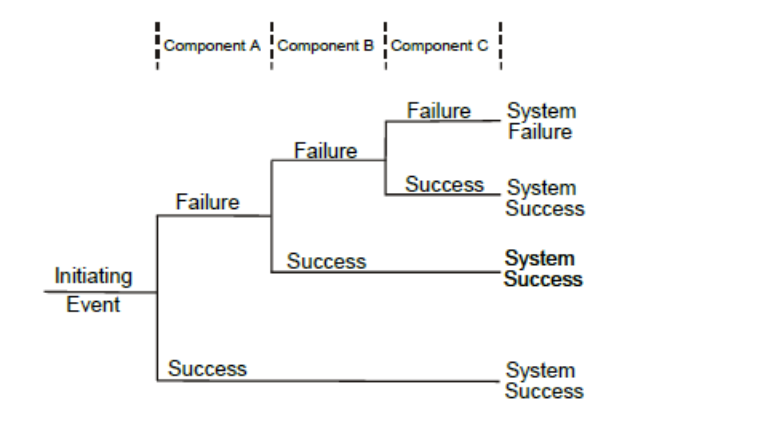
The event tree, shown below, analyses a failsafe

The event tree, shown below, analyses a failsafe mechanism consisting of three (3) components. In the event of a fault, . Component A should operate and correct the If Component A fails to operate, Component B acting as a backup should then operate and correct the If both Component A and Component B fail to respond to the system fault a third back up Component C should operate to correct the The probability of each component failing to operate when required is: o Component A: probability of failure = 0.01 o Component B: probability of failure = 0.001 o Component C: probability of failure = 0.01 Component A Component B Component C C Failure System Failure Failure Failure Success System Success Success Initiating Event System Success Success System Success 1. What is probability that the failsafe system will successfully respond to a fault after the initiating event? 2. Given that the initiating event occurs, what is the probability that Component C will be required to operate? 3. If we wanted to reduce the probability of system failure and we chose to introduce a component D into the system so that both component A and component D had to fail before component B was required to operate, what is the probability that the failsafe system will fail to respond successfully to the initiating event occurring (that is, what is the probability of system failure for this modified system), Component D: probability of failure = 0.0025 A. Draw the event tree for the new system B. Calculate the probability of system failure The event tree, shown below, analyses a failsafe mechanism consisting of three (3) components. In the event of a fault, . Component A should operate and correct the If Component A fails to operate, Component B acting as a backup should then operate and correct the If both Component A and Component B fail to respond to the system fault a third back up Component C should operate to correct the The probability of each component failing to operate when required is: o Component A: probability of failure = 0.01 o Component B: probability of failure = 0.001 o Component C: probability of failure = 0.01 Component A Component B Component C C Failure System Failure Failure Failure Success System Success Success Initiating Event System Success Success System Success 1. What is probability that the failsafe system will successfully respond to a fault after the initiating event? 2. Given that the initiating event occurs, what is the probability that Component C will be required to operate? 3. If we wanted to reduce the probability of system failure and we chose to introduce a component D into the system so that both component A and component D had to fail before component B was required to operate, what is the probability that the failsafe system will fail to respond successfully to the initiating event occurring (that is, what is the probability of system failure for this modified system), Component D: probability of failure = 0.0025 A. Draw the event tree for the new system B. Calculate the probability of system failure

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

A B D F Dayton, Inc. Annual Income Statement (Values in Millions) Common Size 2012 2011 2012 2011 Sales $ 178,909 $ 187,510 Cost of Sales 111.631 Gross Operating Profit Selling, General & Admin....

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

Assignment 1 (a) - 4 Marks 1. Identify at least 10 types of hazards that are to be found in your workplace/industry. Hazard: potential source of harm .. a state or set of conditions of a system ......

uetion1 OECD Health Statistics 2015 Definitions, Sources and Methods HEALTH STATUS (HEALTH_STAT) Access the dataset on Health Status in OECD.Stat:...

Max Weber considers the formal structure as a tool for reaching different goals. This perception is still the hypothesis of many structural analyses, both for practitioners and scientists. The...

1. A photo detector counts photons for 10 nano seconds to decide if a distant light source is emitting light. When the light source is not emitting light, some photons are still counted by the...

2. A photo detector counts photons for 10 nano seconds to decide if a distant light source is emitting light. When the light source is not emitting light, some photons are still counted by the...

Chapter 9 from Business Law and the Legal Environment was adapted by The Saylor Foundation under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 license without attribution as requested...

answer the following questions: What are your moral obligations as professionals to prevent such things from happening? What guidance do the professional codes provide (cite specific code sections in...

A discrete sequence {xn} can be converted into a continuous representation x(t) = ts X n= (t n ts) xn, where ts is the sampling period. (a) State two characteristic properties of Dirac's function. [2...

Research on the Strayer University Library and/or the Internet to identify a company that manufactures products or offers a service. Then investigate the company and its business. Note : In the...

Is the financial community in the U.S. in agreement with the current U.S. GAAP standards as to how to present investment at fair value (often called mark-to-market accounting)? What impact did these...

Which one of the following statements is accurate for a levered firm? Multiple Choice The subjective approach totally ignores a firm's own WACC. A reduction in the risk level of a firm will tend to...

Read the articles on journaling and review the template provided. Identify what approach, to journaling, in the articles you found useful and why. Post to the discussion forum that you have reviewed...