The extended Euclidean algorithm is used for efficiently finding the multiplicative inverse (when it exists; Note that when we are looking for the multiplicative inverse of a mod n, gcd(a,n) needs to be 1.) We run the Euclidean algorithm as before but in addition to q₁,q₂,...r₁,r₂,... we also compute s_i and t_i where;

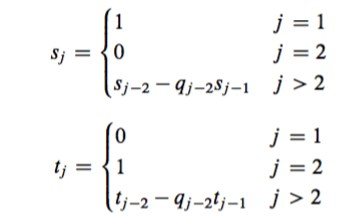
Write a C++ program that takes two positive integers as input. First, it checks if the

gcd of them is 1, if so, then it should return the multiplicative inverse of the

second input argument. You need to print a trace of your program as well. For

example, if your input values are 28; 75, the multiplicative inverse of 28 mod 75

is -8 =75 67 and the trace table looks like the following.

i	qi	ri	ri + 1	ri +2	si	ti
1	2	75	28	19	1	0
2	1	28	19	9	0	1
3	2	19	9	1	1	-2
4	9	9	1	0	-1	3
5		1			3	-8

9-2-qj-29-1 J >2 6-2-%-2tj-1 J >2 122 122 10 01