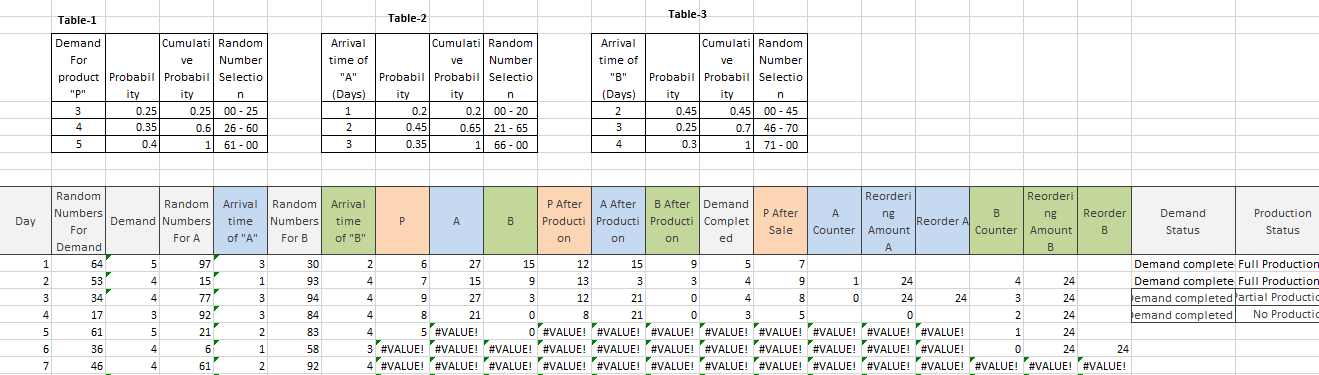
the first pic is how the simulation should be. please i need the formula for each column as soon as possible

Table-3 Table-1 Table-2 ve Demand Cumulati Random For ve Number product Probabil Probabil Selectio "P" ity ity n 3 0.25 0.25 00 - 25 4 0.35 0.6 26-60 5 0.4 61 - 00 Arrival time of "A" (Days) 1 2 3 Cumulati Random ve Number Probabil Probabil Selectio ity ity n 0.2 0.21 00 - 20 0.45 0.65 21 - 65 0.35 1 66 - 00 Arrival time of "B" (Days) 2 3 4 Cumulati Random Number Probabil Probabil Selectio ity ity n 0.45 0.45 00 - 45 0.25 0.7| 46 - 70 0.3 1 71 - 00 1 Day Random Random Arrival Random Numbers Demand Numbers time Numbers For For A of "A" For B Demand 1 64 5 97 3 30 2 53 4 157 1 93 3 34 4 77' 3 94 4. 17 3 927 3 84 5 61 5 21 2 83 6 36 4 61 1 58 7 46 4 61 2 92 Arrival P After Reorderi Reorderi A After B After Demand P After B ng time ng Reorder Demand Production Producti Producti Producti Complet Reorder All Sale Counter of "B" Amount Counter Amount B Status Status on on on ed B 2 6 27 15 12 15 9 5 7 Demand complete Full Production 4 7 15 9 13 3 3 4 9 1 24 4 24 Demand complete Full Production 4 9 27 3 12 21 o 4 8 0 24 24 24 emand completed artial Productie 4 8 21 0 8 21 0 3 5 0 2 24 emand completed No Productid 4 5 #VALUE! O #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 1 24 3 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 0 24 24 4 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 3 In a factory a certain product "P" is produced. Maximum 6 "P"s can be produced in a day providing there are enough materials. Two parts of material "A" and one part of material "B" are used to preoduce one "P". Partial production is possible depending on number of materials "A" and "B". When there is not enough material the production stops. The product "P" is offered for sale. The demand for product "P" is randomly distributed as shown in Table-1. The parts "A" and "B" are imported from abroad and the time of their arrival are at random as shown in Table-2 and Table-3. In the beginning of the simulation experiment there are 3 finished products "P", 27 "A"s and 15 "B"s in stock. Minimum reorder levels of parts "A" and "B" are 12 and 6 respectively. When the parts "A" and "B" arrive they can be used in production immediately. After 30 days of simulation answer the following. a) Number of days with full production b) Partial Production c) No production d) Total Number of demands e) Sales f) Total number of days demand not met. Table-3 Table-1 Table-2 ve Demand Cumulati Random For ve Number product Probabil Probabil Selectio "P" ity ity n 3 0.25 0.25 00 - 25 4 0.35 0.6 26-60 5 0.4 61 - 00 Arrival time of "A" (Days) 1 2 3 Cumulati Random ve Number Probabil Probabil Selectio ity ity n 0.2 0.21 00 - 20 0.45 0.65 21 - 65 0.35 1 66 - 00 Arrival time of "B" (Days) 2 3 4 Cumulati Random Number Probabil Probabil Selectio ity ity n 0.45 0.45 00 - 45 0.25 0.7| 46 - 70 0.3 1 71 - 00 1 Day Random Random Arrival Random Numbers Demand Numbers time Numbers For For A of "A" For B Demand 1 64 5 97 3 30 2 53 4 157 1 93 3 34 4 77' 3 94 4. 17 3 927 3 84 5 61 5 21 2 83 6 36 4 61 1 58 7 46 4 61 2 92 Arrival P After Reorderi Reorderi A After B After Demand P After B ng time ng Reorder Demand Production Producti Producti Producti Complet Reorder All Sale Counter of "B" Amount Counter Amount B Status Status on on on ed B 2 6 27 15 12 15 9 5 7 Demand complete Full Production 4 7 15 9 13 3 3 4 9 1 24 4 24 Demand complete Full Production 4 9 27 3 12 21 o 4 8 0 24 24 24 emand completed artial Productie 4 8 21 0 8 21 0 3 5 0 2 24 emand completed No Productid 4 5 #VALUE! O #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 1 24 3 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 0 24 24 4 #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! 3 In a factory a certain product "P" is produced. Maximum 6 "P"s can be produced in a day providing there are enough materials. Two parts of material "A" and one part of material "B" are used to preoduce one "P". Partial production is possible depending on number of materials "A" and "B". When there is not enough material the production stops. The product "P" is offered for sale. The demand for product "P" is randomly distributed as shown in Table-1. The parts "A" and "B" are imported from abroad and the time of their arrival are at random as shown in Table-2 and Table-3. In the beginning of the simulation experiment there are 3 finished products "P", 27 "A"s and 15 "B"s in stock. Minimum reorder levels of parts "A" and "B" are 12 and 6 respectively. When the parts "A" and "B" arrive they can be used in production immediately. After 30 days of simulation answer the following. a) Number of days with full production b) Partial Production c) No production d) Total Number of demands e) Sales f) Total number of days demand not met