the first question tq

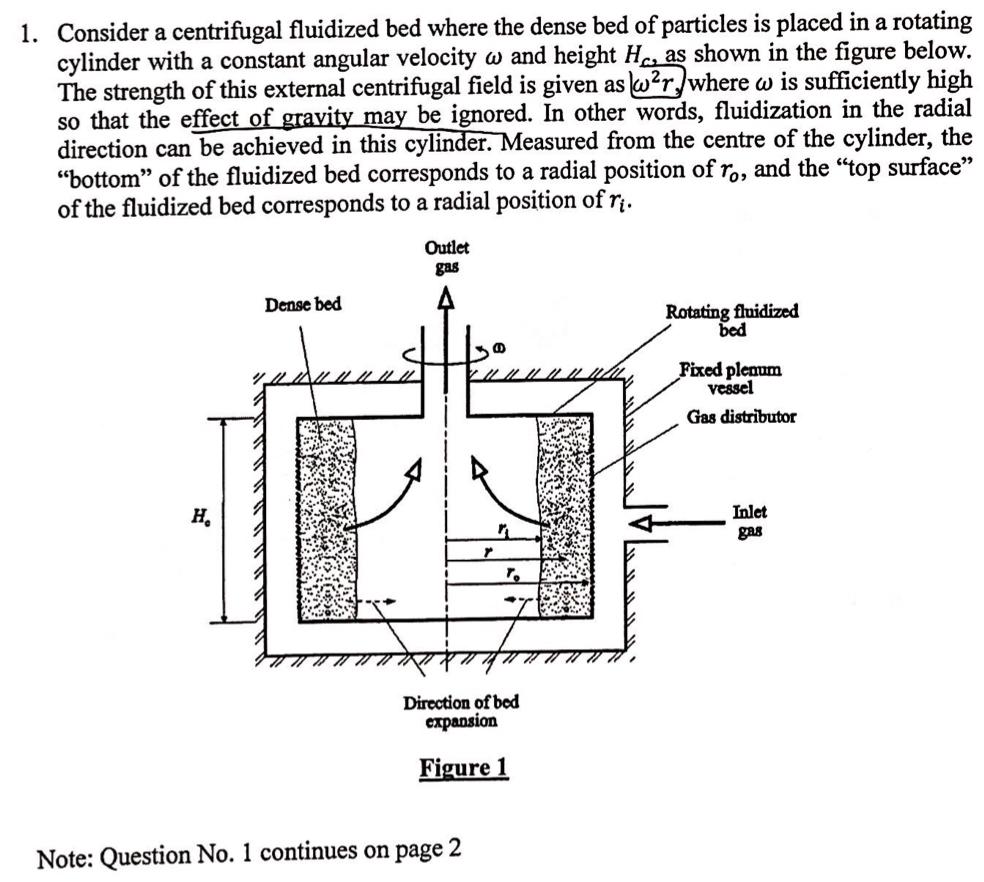
1. Consider a centrifugal fluidized bed where the dense bed of particles is placed in a rotating cylinder with a constant angular velocity w and height Hc, as shown in the figure below. The strength of this external centrifugal field is given as War)where w is sufficiently high so that the effect of gravity may be ignored. In other words, fluidization in the radial direction can be achieved in this cylinder. Measured from the centre of the cylinder, the "bottom of the fluidized bed corresponds to a radial position of r., and the "top surface of the fluidized bed corresponds to a radial position of ri. Outlet gas Dense bed Rotating fluidized bed HE Fixed plenum vessel Gas distributor H. Inlet gas r Direction of bed expansion Figure 1 Note: Question No. 1 continues on page 2 a) Assume is a constant throughout the dense-phase bed, rewrite the following equation we are used to for conventional fluidized beds for this rotating fluidized bed, then integrate it to obtain an expression of total pressure drop AP across the bed, as a function of ro, ri and other constants. dp [(1 )(pp - Ps)]g dH (8 marks) b) Based on the geometry of this rotating cylinder, derive an expression for the total mass of particles in the bed. (8 marks) c) Rewrite the differential form of the Ergun equation for the system, and then integrate it to obtain the Ergun equation for this centrifugal fluidized bed. Assume that the gas superficial velocity at r., location of the gas distributor, is a constant, which can simply be denoted as Umf. dP (1 )? U = 150 1 - E pqU2 + 1.75 dH ?d; E3 3 (Hint: Take note that gas is flowing in the radial direction, so is U still a constant throughout the bed.) (9 marks)