The Floyd-Warshall algorithm for computing all-pairs shortest paths computes a table of values dist(i, j, k), giving the length of the shortest path from i to j that does not include any intermediate vertices numbered higher than k.

The pseudocode for the Floyd-Warshall algorithm:

Now refer to this graph:

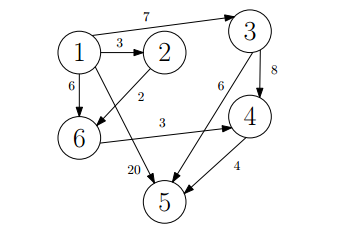
(a) Give the value of dist(1, 5, 3) for the above graph.

(b) When the Floyd-Warshall algorithm computes the value of dist(1, 5, 4) which previously computed dist(i, j, k) table entries does it access?

for i=1 to n: for j l to : dist(i, j,0)=00 dist(i j. 0)ij) for i 1 to n: for all ij)EE for k=1 to n: for j l to n: dist(i, j. k)=min/dist[i, k k11+dist(k, j, k-1), dist(i, j, k-1))