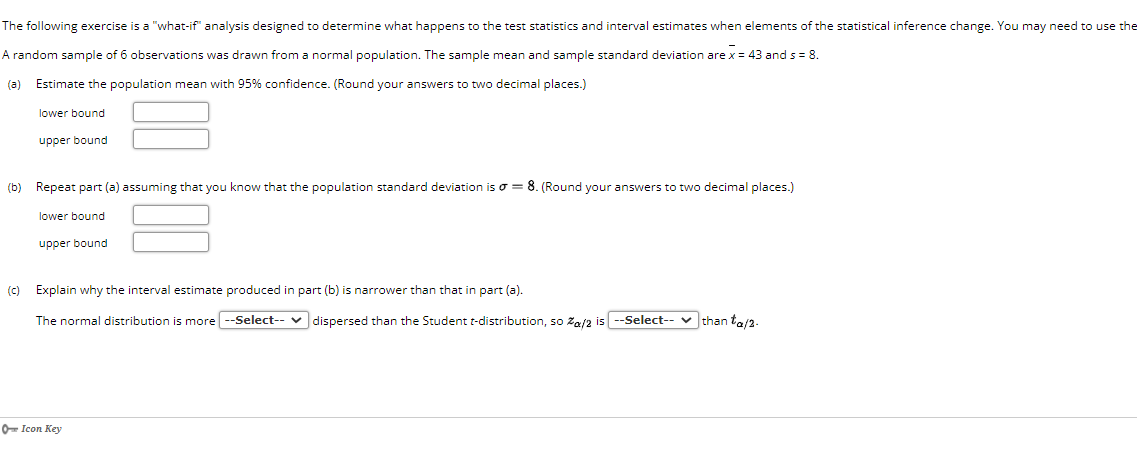
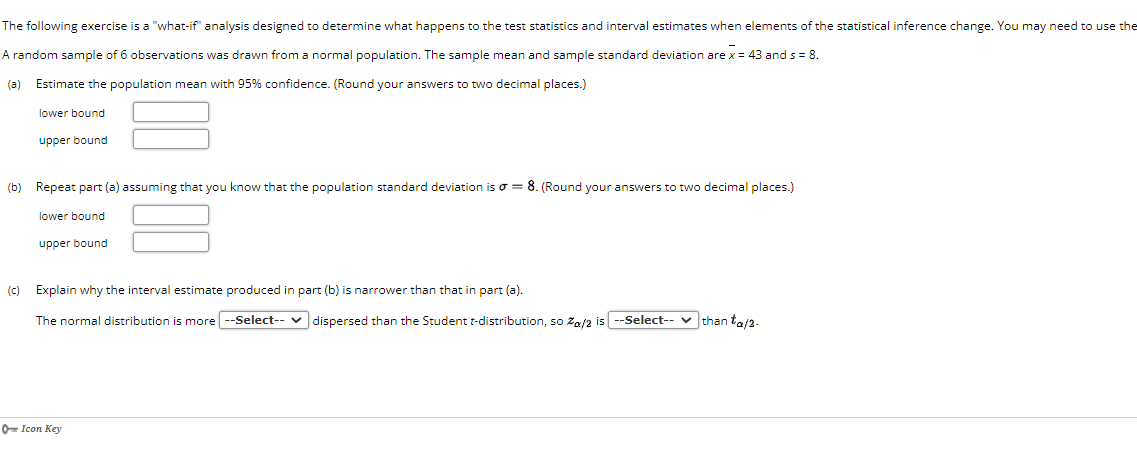
The following exercise is a "what-if" analysis designed to determine what happens to the test statistics and interval estimates when elements of the statistical inference change. You may need to use the A random sample of 6 observations was drawn from a normal population. The sample mean and sample standard deviation are x = 43 and s = 8. (a) Estimate the population mean with 95% confidence. (Round your answers to two decimal places.) lower bound upper bound (b) Repeat part (a) assuming that you know that the population standard deviation is 7 = 8. (Round your answers to two decimal places.) lower bound upper bound (c) Explain why the interval estimate produced in part (b) is narrower than that in part (a). The normal distribution is more |--Select-- |dispersed than the Student t-distribution, so Za/2 is --Select-- v than to/2. O- Icon Key