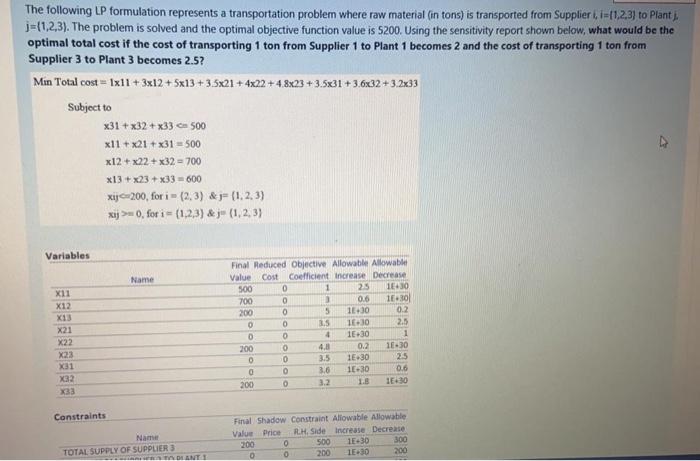
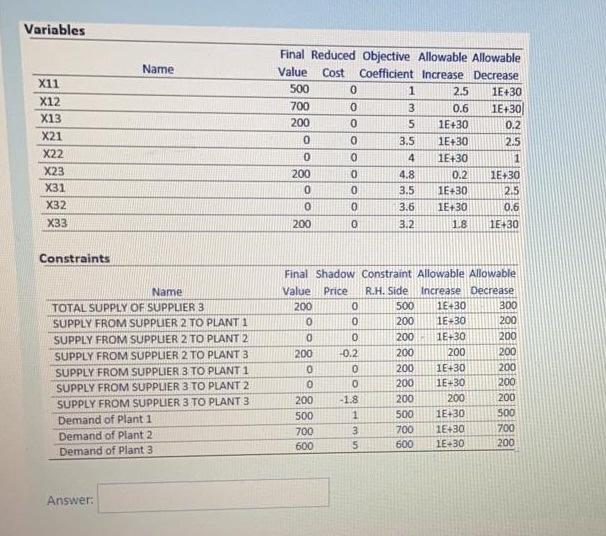
Question: The following LP formulation represents a transportation problem where raw material (in tons) is transported from Supplier =(1,2,3) to Planti. j={1,2,3). The problem is solved
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


