Question: The function f(x,y) = 3xy has an absolute maximum value and absolute minimum value subject to the constraint 3x2 + 3y- - 5xy = 121.

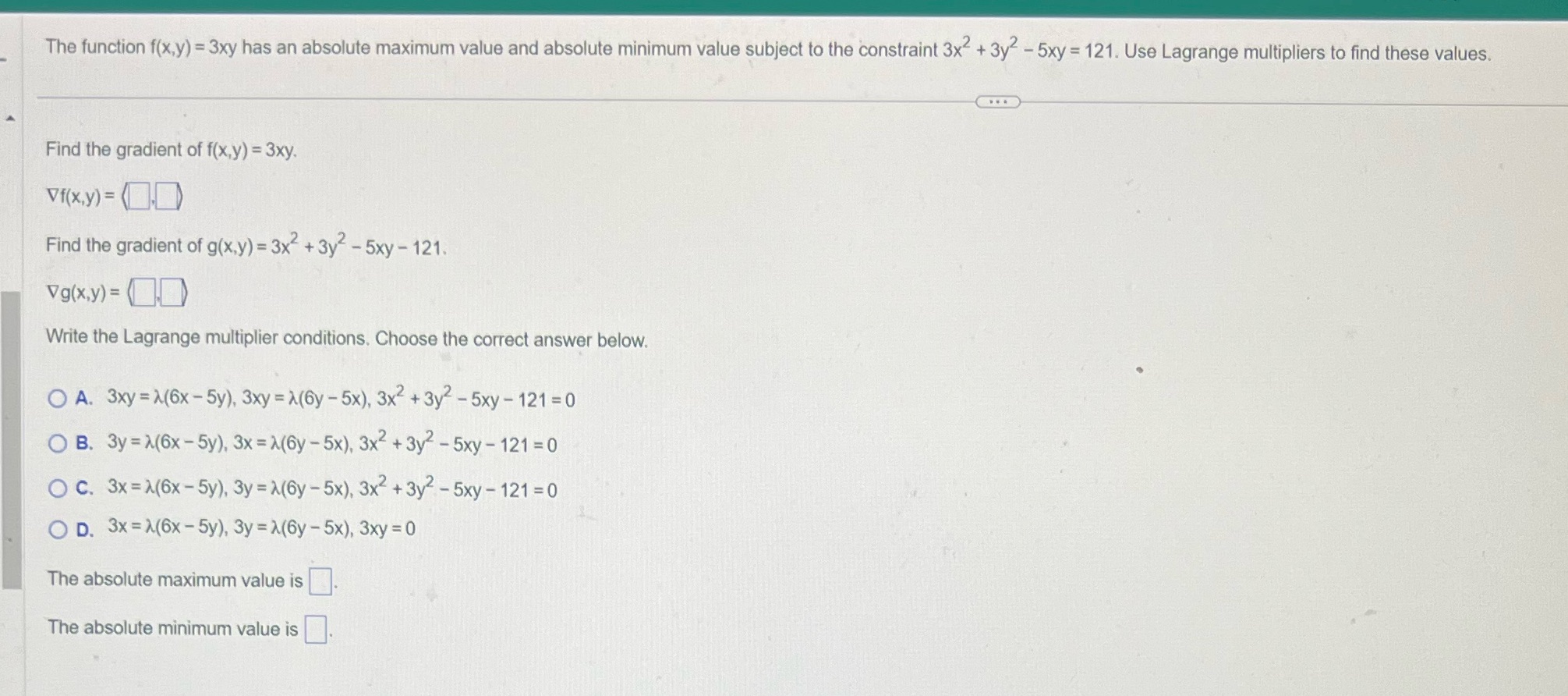
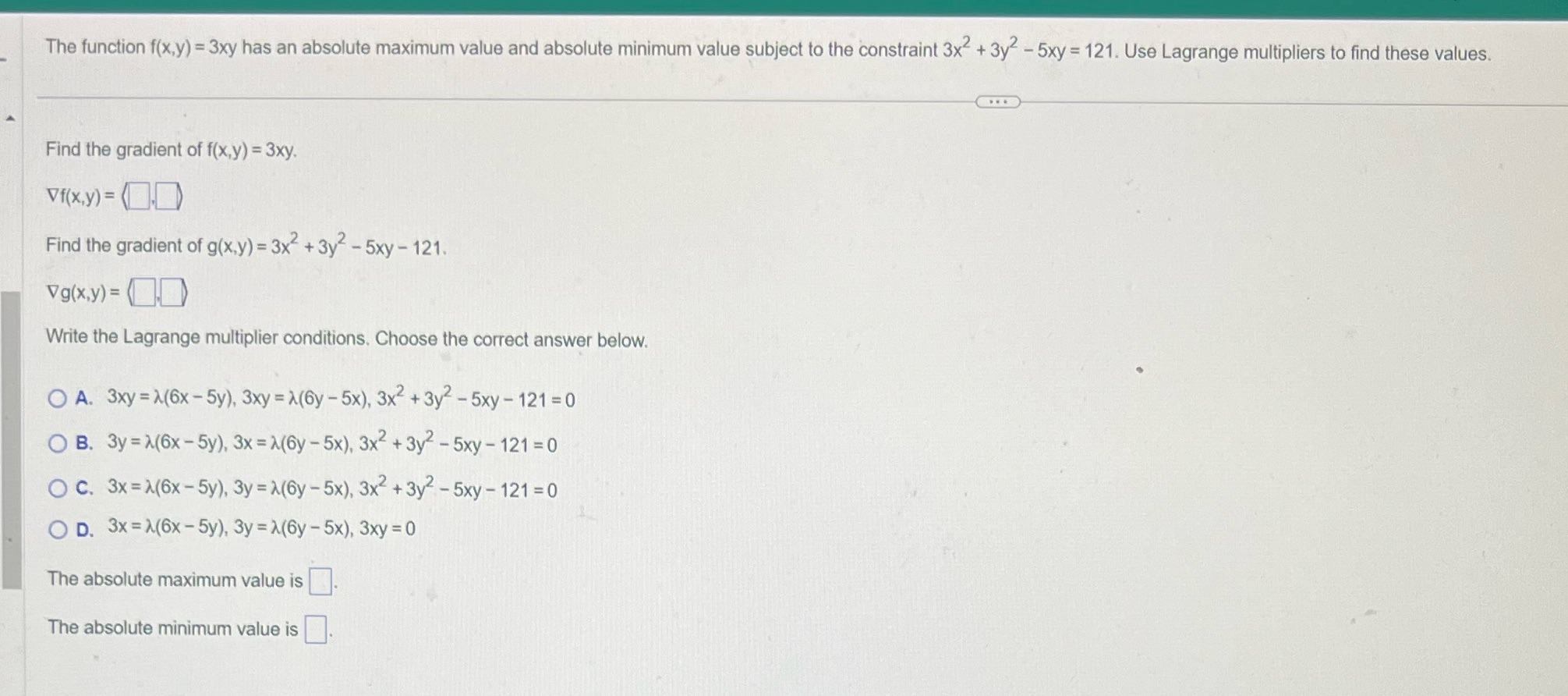
The function f(x,y) = 3xy has an absolute maximum value and absolute minimum value subject to the constraint 3x2 + 3y- - 5xy = 121. Use Lagrange multipliers to find these values. Find the gradient of f(x,y) = 3xy. Vf(x,y) => Find the gradient of g(x,y) = 3x2+ 3y2-5xy -121. Vg(x,y) = Write the Lagrange multiplier conditions. Choose the correct answer below. O A. 3xy = >(6x - 5y), 3xy = >(6y - 5x), 3x2 + 3y2-5xy - 121 =0 O B. 3y = >(6x - 5y). 3x = >(6y - 5x), 3x2 + 3y2 - 5xy - 121 = 0 O C. 3x = >(6x - 5y), 3y = >(6y - 5x), 3x2 + 3y2- 5xy - 121 =0 O D. 3x = >(6x - 5y), 3y = >(6y - 5x), 3xy = 0 The absolute maximum value is The absolute minimum value is

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The function f(x,y) = 3xy has an absolute maximum value and absolute minimum value subject to the constraint 3x2 + 3y2 -5xy=121. Use Lagrange multipliers to find these values

I point(s) possible The function f(x,y,z) = 7x - 4y + 5z has an absolute maximum value and absolute minimum value subject to the constraint x+ y+ z=90. Use Lagrange multipliers to find these values....

The function f(x,y,z) = 8x - 4y + z has an absolute maximum value and absolute minimum value subject to the constraint x2+ y2 + z? =81. Use Lagrange multipliers to find these values. Find the...

The function f(x,y) = 4xy has an absolute maximum value and absolute minimum value subject to the constraint 2x- + 2y- - 3xy = 49. Use Lagrange multipliers to find these values. Find the gradient of...

The function f(x,yz) = 5x has an absolute maximum value and absolute minimum value subject to the constraint x- + y- + z" -5z = 5. Use Lagrange multipliers to find these values. The maximum value...

The function f(x,y) = xy has an absolute maximum value and absolute minimum value subject to the constraint 2x2 + 2y2 - 3xy =49. Use Lagrange multipliers to find these values. . .. Find the gradient...

The function f(x,y) = 2xy has an absolute maximum value and absolute minimum value subject to the constraint 3x2 + 3y2-5xy= 121. Use Lagrange multipliers to find these values. . . . Find the gradient...

The function f(x,y) = 7xy has an absolute maximum value and absolute minimum value subject to the constraint x" + y- - xy =9. Use Lagrange multipliers to find these values. Find the gradient of...

The function f(x,y) = 2xy has an absolute maximum value and absolute minimum value subject to the constraint 3x" + 3y" - 5xy = 121. Use Lagrange multipliers to find these values. The absolute maximum...

1. The function f(x,y) = 4xy has an absolute maximum value and absolute minimum value subject to the constraint 2x2 + 2y -3xy =49. Use Lagrange multipliers to find these values. The absolute maximum...

Eight solid plastic cubes, each 3.00 cm on each edge, are glued together to form each one of the objects (i, ii, iii, and iv) shown in Figure P23.37. (a) Assuming each object carries charge with...

Chemical kinetics does not involve research in the following areas: a) chemical reaction rate; b) Factors affecting the reaction rate; c) The mechanism of the reaction; d) Energy as a reaction...

Create a project consisting of three classes. These three classes are named ProgTwo.java, Product.java and ProductCollection.java. You must have these three classes and they must work as it is...

The force constant of a massless spring is 2 5 . 0 N / m . A mass of 0 . 4 5 kg is oscillating in simple harmonic motion at the end of the spring

Describe a situation in which you have demonstrated elements of the personal journey disciplines to achieve a goal. What were your strengths, and what would you like to develop more fully?

How does a complex adaptive system affect day-to-day decision making? What factors need to be taken into account when creating a climate for change?

What impact does having knowledge of evidence-based practice have on the overall healthcare climate of the organization?