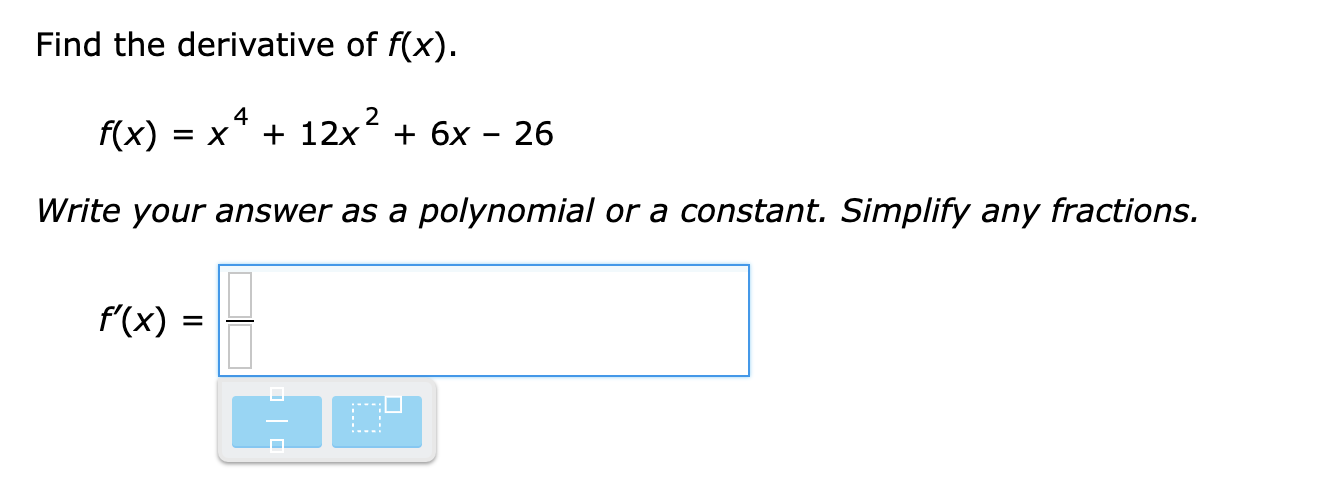
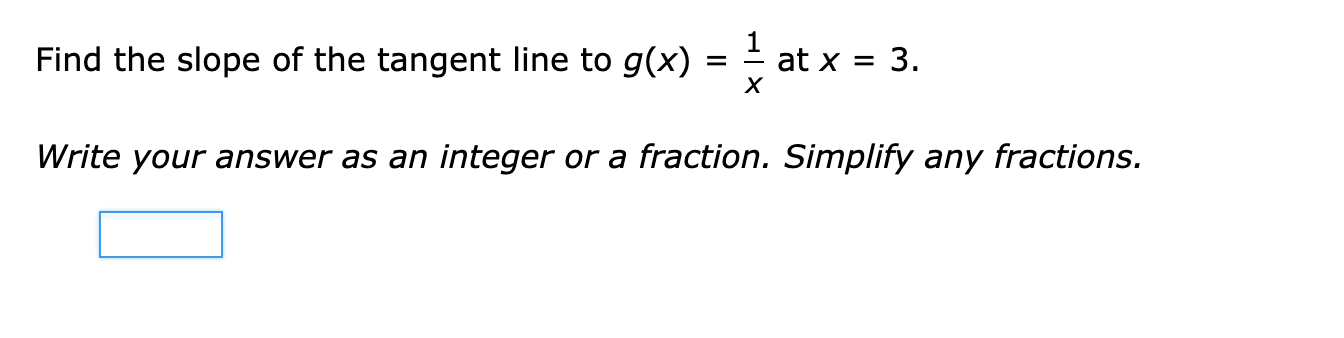
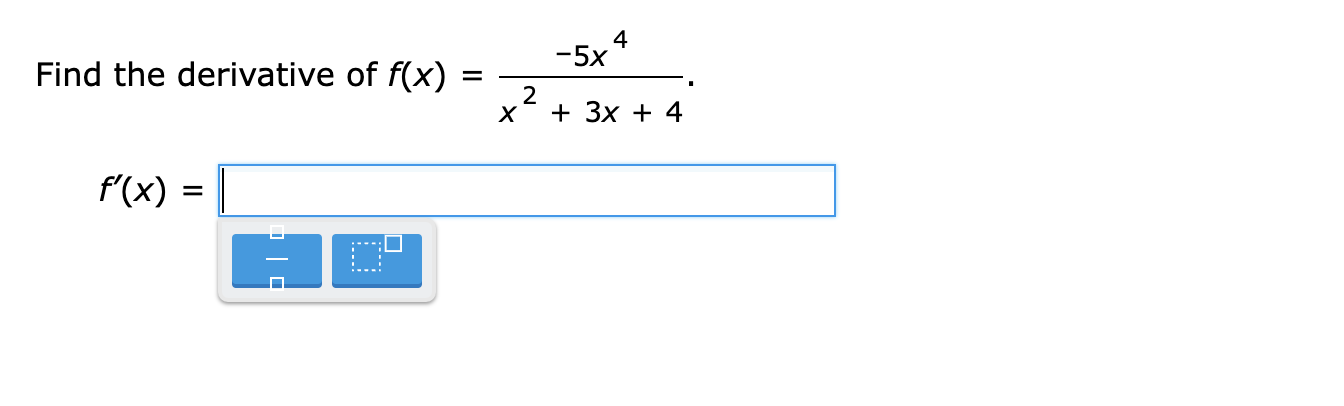
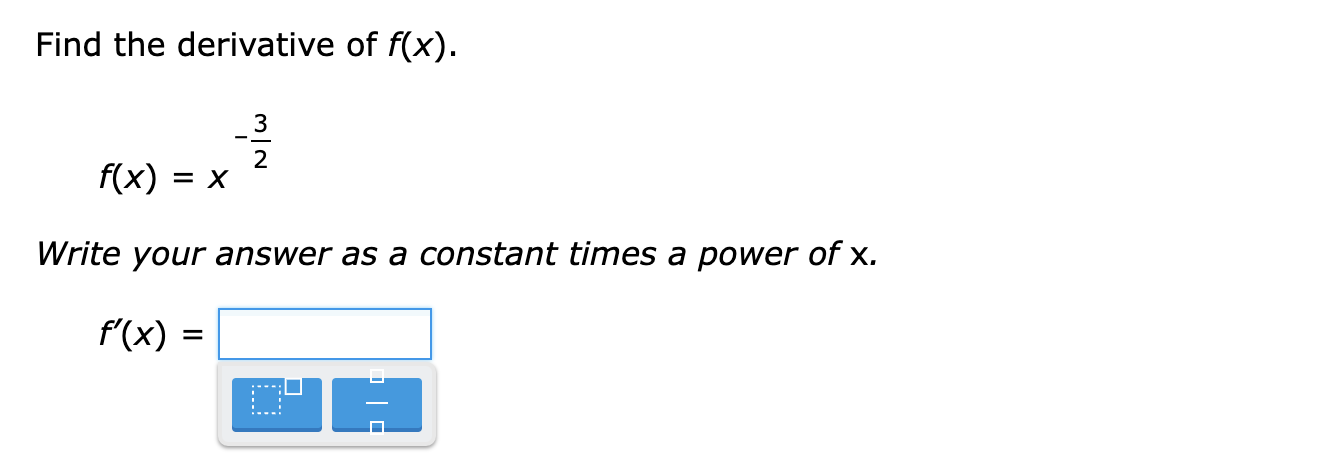
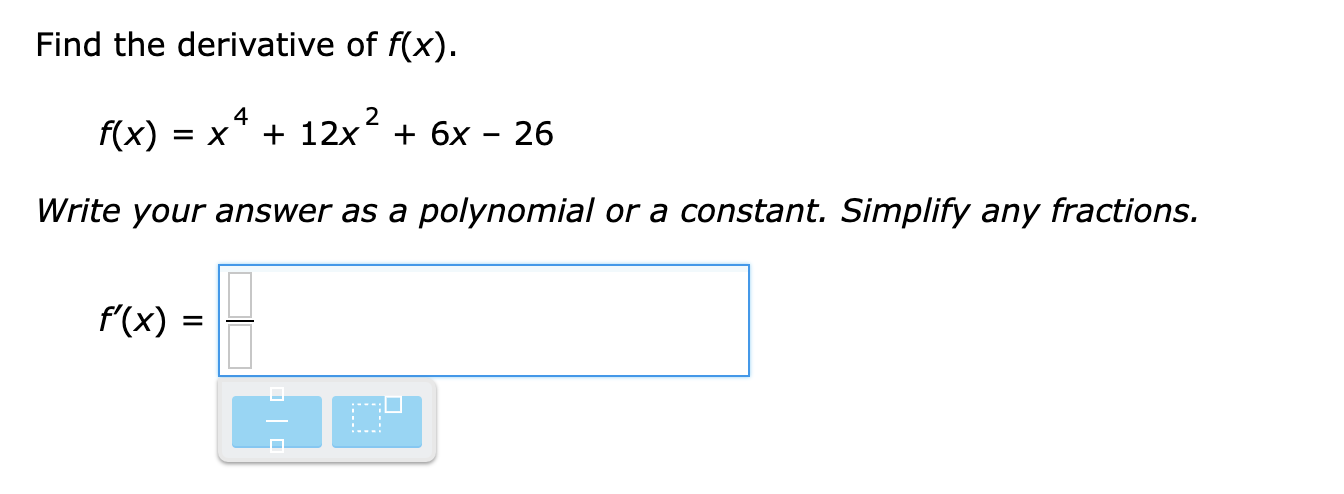
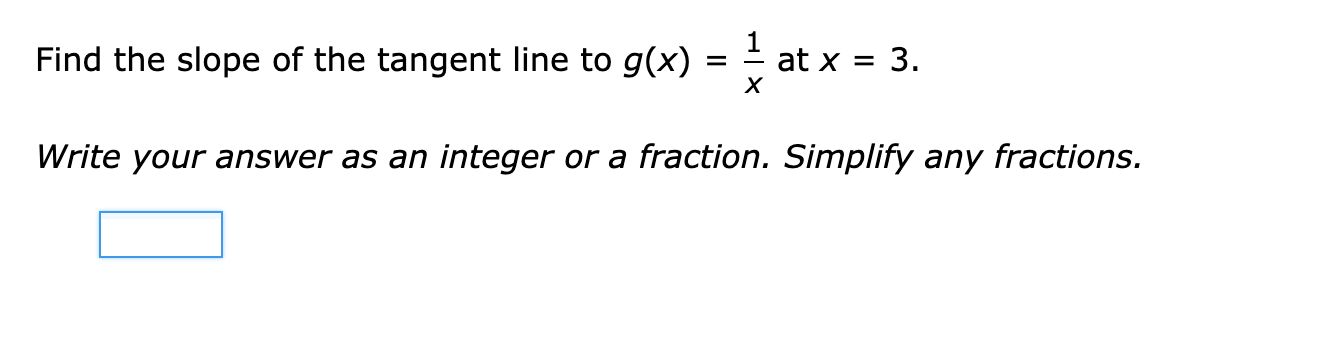
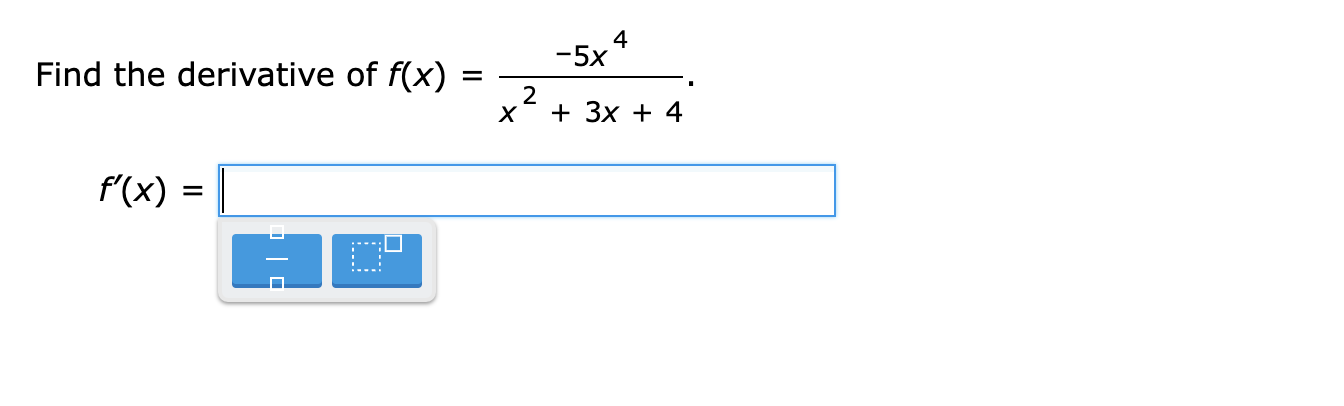
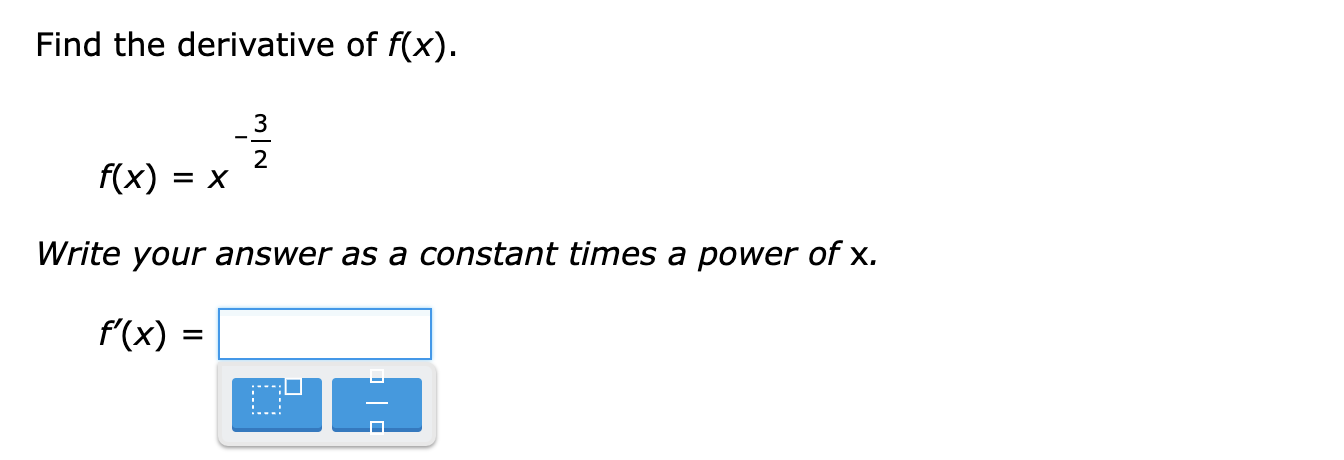
The function g(x) is differentiable. The function h(x) is defined as: h = L (X) 900 If 9(1) = -4 and g'(1) = -7, what is h'(1)? Simplify any fractions. h'(1)= E Find the derivative of f(x). f(x) =x4 + 12x2 + 6x- 26 Write your answer as a polynomial or a constant. Simplify any fractions. The function f(X) is differentiable. The function h(x) is defined as: h(x) = xf(x) If f(-3) = 7 and f'(-3) = -8, what is h'(-3)? Simplify any fractions. h'(-3) = E Find the derivative of f(x). f( x) = x-5 Write your answer as a constant times a power of x. f'( x ) =Find the derivative of f(x). f(x) = W Write your answer as a constant times a power of x. m = E The function g(x) is differentiable. The function h(x) is defined as: h(x) = i 900 If 9(7) = -2 and g'(7) = 3, what is h'(7)? Simplify any fractions. W) = E The functions f(x) and 90:) are differentiable. The function h(x) is defined as: h(x) = 2f(x) + 7g(x) If f(-7) = -6, f'(-7) = 5, g(-7) = -3 and g'(-7) = 10, what is h'(-7)? Simplify any fractions. h'(-7) = E Find the equation of the tangent line to k(x) = 21 X2 at X = 5. Simplify any fractions. The functions f(x) and g(X) are differentiable. The function h(x) is defined as: h(x) = 5f(x) + 6g(x) If f(4) = '9, f'(4) = 6, 9(4) = 9 and g'(4) = -10, what is h'(4)? Simplify any fractions. h'(4) = Find the slope of the tangent line to g(x) = i at X = 3. Write your answer as an integer or a fraction. Simplify any fractions. E Find the derivative of f(x). f(x) = -2x12 + 3X8 + 5X3 + 3x2 25 Write your answer as a polynomial or a constant. Simplify any fractions. rm = E lil mil The function g(x) is differentiable. The function h(x) is defined as: h(X) = X9(X) If 9(8) = -9 and g'(8) = 2, what is h'(8)? Simplify any fractions. m) = E \fFind the derivative of f(x). 3 f(x) = x 3 Write your answer as a constant times a power of x. we = : mil lil \fFind the derivative of f(x). -6 f( x ) = X U X Write your answer as a constant times a power of x. f'( x ) =