The Gamma function is defined for > 0 by () = (0,) x^(1)*e^x dx.

A Beta random variable with parameters > 0 and > 0 is the random variable with density f(x) = ( ( + ) / ()() )* x^(1)*(1 x)^(1) if 0

(If = = 1 the Beta random variable is a uniform random variable on the interval (0, 1)). Suppose that X is a Beta random variable with parameters and .

(a) Show that E(X) = + .

(b) Find Var(X).

Screenshot of the problem in case of confusion

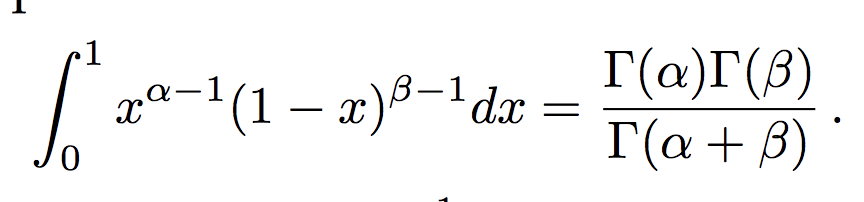
Problem 5. A Beta random variable with parameters 04 > 0 and B > 0 is the random variable with density Na + B) 1 51 a: = a:' 1 a: f ( ) F( 0011(5) ( ) if 0