Question: The graph below shows the base of an object. Compute the exact value of the volume of the object, given that cross sections (perpendicular

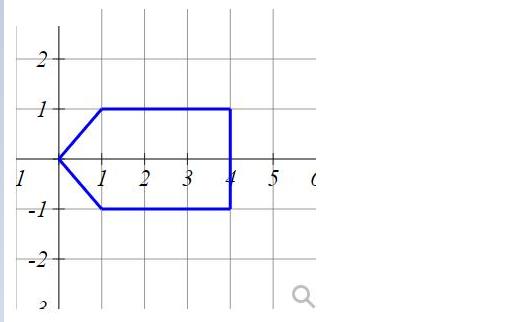
The graph below shows the base of an object. Compute the exact

value of the volume of the object, given that cross sections (perpendicular

to the base and parallel to the y-axis) are isosceles right triangles

The graph below shows the base of an object. Compute the exact value of the volume of the object, given that cross sections (perpendicular to the base and parallel to the y-axis) are isosceles right triangles with their hypotenuse in the base. V 6.2857 no decimals allowed. = X 1 1 -1 ( Let C be the curve y = 24 21 18- 15 12 a 6- 3 e2.4x First find and simplify +e 4.8 2.4x 0.25 0.5 0.75 1 1.25 1.5 1.75 2 Find the surface area of revolution about the x-axis of C. /1+ y for 0.6 x 1.7. A graph containing C follows. " Now find surface area = 3.2353 x e2.4x + e-2.4x 2

Step by Step Solution

★★★★★

3.26 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To find the volume of the object described by the graph we can use the method of crosssectional area... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

E4-21 Reporting an Income Statement, Statement of Stockholders Equity, and Balance Sheet LO4-2 Green Valley Company prepared the following trial balance at the end of its first year of operations...

The graph below shows the time it takes Quick Pain Relief to relieve a persons pain. The graph below that shows the time a competitors product takes to relieve pain. Why might these graphs be...

The graph below shows six different curves labeled AF. Each curve shows the relationship between the p-value (y-axis) and the distance pË Ï (x-axis) for testing the null hypothesis Ï =...

Let C be the curve r(t) = (t cos t, t sin t, t). Show that C lies on the cone x2 + y2 = z2. Sketch the cone and make a rough sketch of C on the cone.

Let R be the region bounded by the graphs of f ( x) = 6/x+2 and g(x)=4, and the vertical line x=1. Region R is the base of a solid. Cross sections perpendicular to the y-axis are isosceles right...

Let R be the region bounded by the graphs of f(x)=6/x+2, g(x)=4, and the vertical line x=1. Region R is the base of a solid. Cross sections perpendicular to the y-axis are isosceles right triangles...

Let R be the region enclosed by the graphs of f(x)=x, the horizontal line y=0, and the vertical line x=8. Region R is the base of a solid. Cross sections perpendicular to the x-axis are isosceles...

O 7 6 2 1 2 3 6 2 The graph above shows the base of an object Compute the value of the volume of the object given cross sections perpendicular to the base are squares Give an exact expression or...

Let S be the solid with flat base, whose base is the region in the a: 1; plane defined by the curves y : em, 3; : 72, m : 1 and a: : 2, and whose cross sections perpendicular to the 2 axis are...

Let R be the first quadrant region bounded by the graphs of f(x)=2x(4-x), and the x-axis. Region R is the base of a solid . Cross sections perpendicular to the x axis are equilateral triangles with...

The base of a solid is the region bounded by y = x^2 and y = 4 . Find the volume of the solid given that the cross sections perpendicular to the x axis are: equilateral triangles

Q8. What are the 7P's in Service Marketing Mix? Explain in details the significance in service industry. Marks: 15

The Excel file Blood Pressure shows the monthly blood pressure (diastolic) readings for a patient before and after medication. a. Test the hypothesis that the variances of monthly blood pressure...

A lumber company purchases and installs a wood chipper for $200,000. The chipper is classified as MACRS 7-year property. The chippers useful life is 10 years. The estimated salvage value at the end...

Part variability is critical in the manufacturing of ball bearings. Large variances in the size of the ball bearings cause bearing failure and rapid wearout. Production standards call for a maximum...

The average grass maintenance engineer mows 1.4 acres of grass per day in Barron, Montana. Because labor costs are increasing, the city decides to try a new brand of mower. Ten randomly selected...

On January 1, 2018, White Water issues $600,000 of 7% bonds, due in 10 years, with interest payable annually on December 31 each year. Required: Assuming the market interest rate on the issue date is...

The following ledger accounts are for Afocentric Service Company: a. Supplies b. Utilities Expense c. Accounts Receivable d. D. Minimus, Capital e. Land f. Prepaid Rent g. Accounts Payable h....

Prepare General Journal entries to record the following August 2014 transactions of a new business called The Pixel Shop. Aug. 1 Joseph Eetok, the owner, invested $20,000 cash and photography...

Presenta tu analisis en un cuadro comparativo considerando lo siguiente: 1. 2. Se debe describir, como introduccin al cuadro comparativo, qu son los mtodos directos e indirectos. Descripcidn de las...

In a randomized, double-blind study reported in the Journal of American Medical Association, researchers Waber et al. (2008) administered a pill to each of 82 healthy paid volunteers from Boston,...

Each singer in the New York Choral Society in 1979 self-reported his or her height to the nearest inch. Their voice parts in order from highest pitch to lowest pitch are Soprano, Alto, Tenor, and...

In Exploration 8.2B, we will look at a study that was done to determine if there is an association between the amount of light in infants bedrooms at night (darkness, night light, room light) and...

Calculate the missing value.

In February of 2008, Twitter.com had 475,000 unique visitors. In February of 2009, this figure had grown by 1382%. How many unique visitors did Twitter have in February of 2009 (rounded to the...

What was the percent change in unit price when the regular size of Lily soap bars dropped from 100 g to 90 g (with no change in the price per bar)?