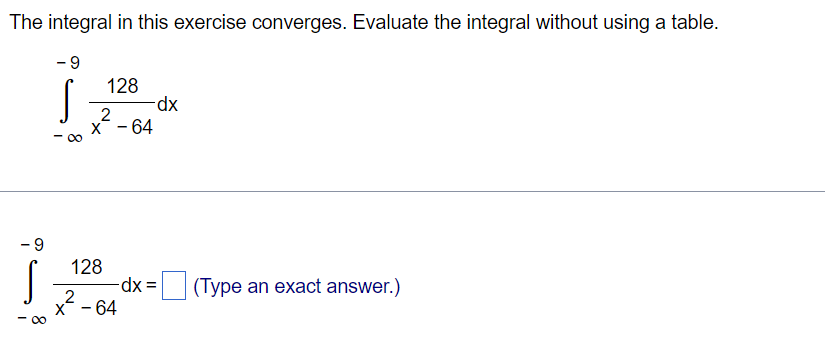
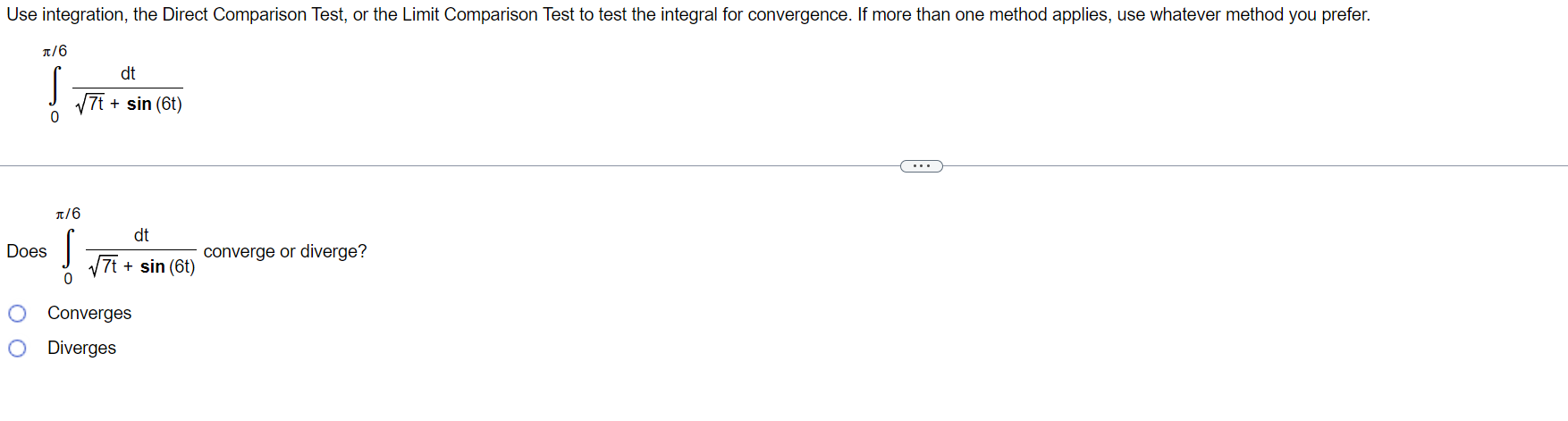
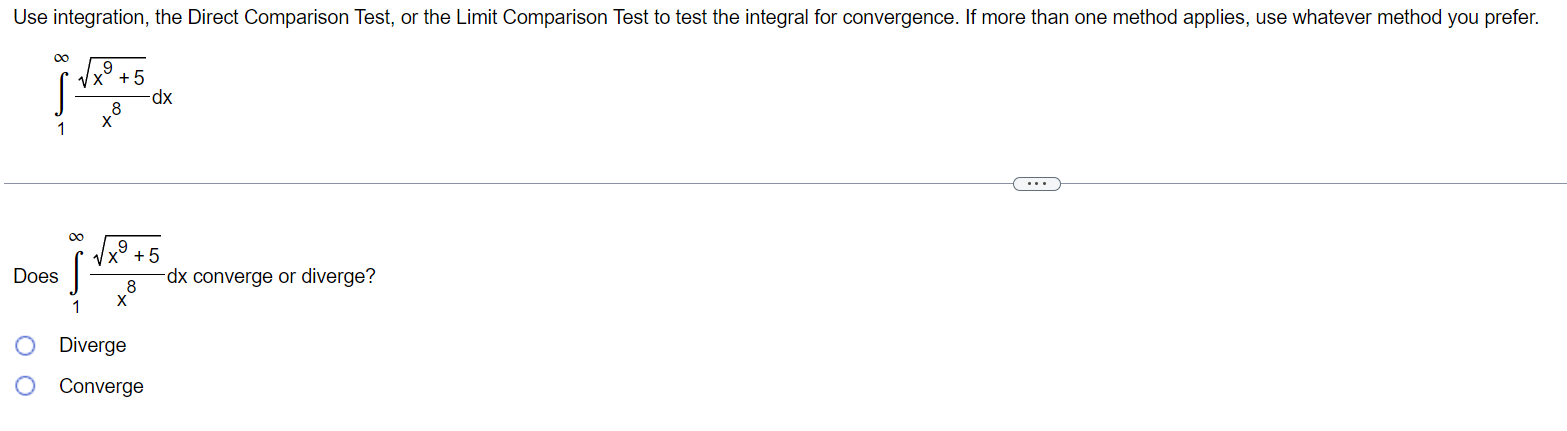
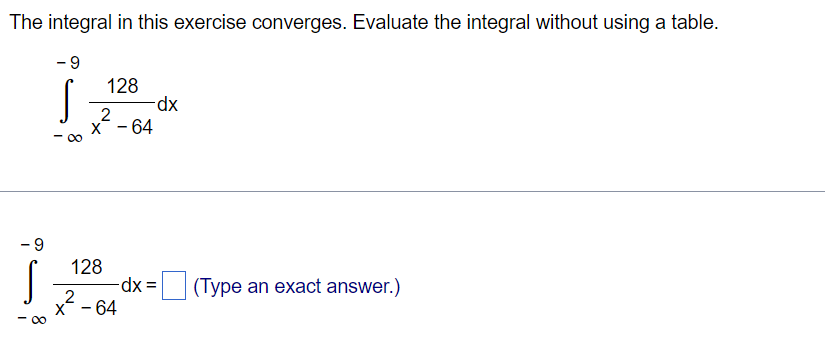
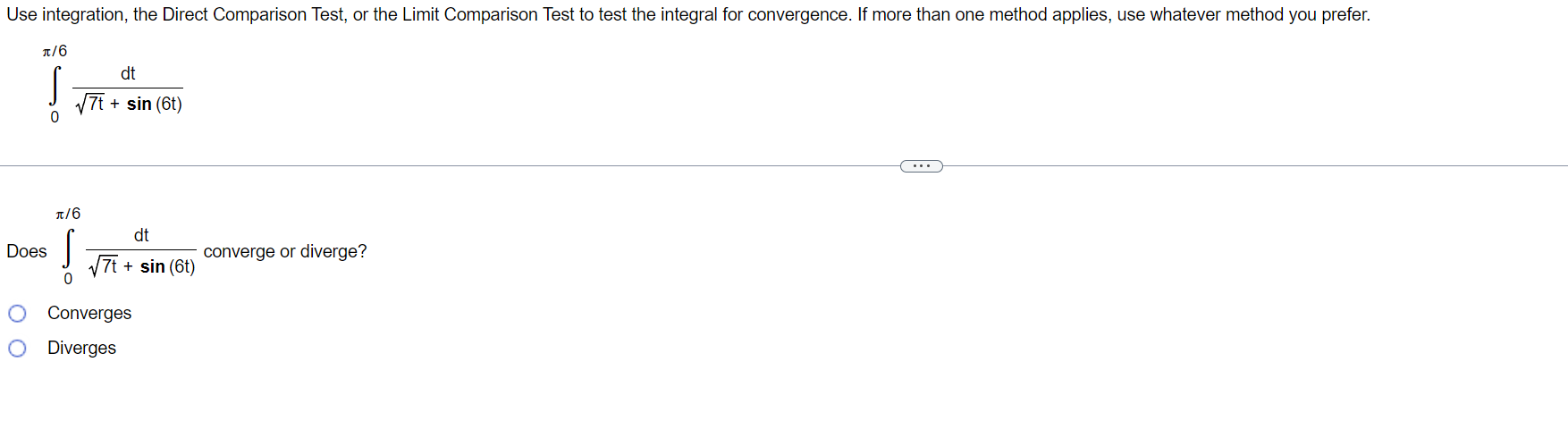
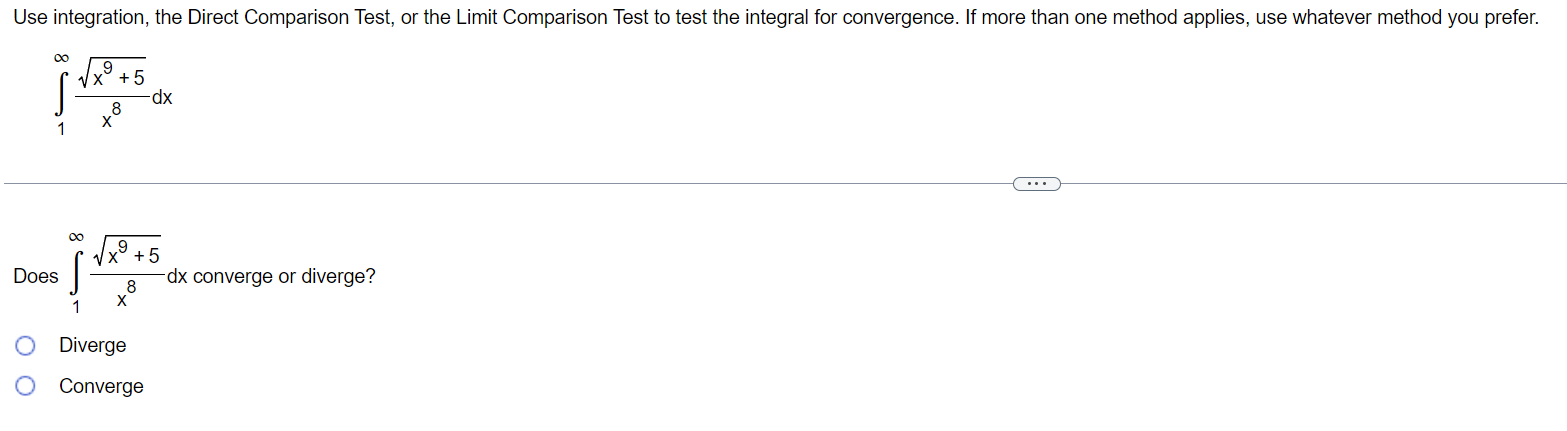
The integral in this exercise converges. Evaluate the integral without using a table. -9 I 128 d X m 3:2 s4 -9 128 I 2 dx = E (Type an exact answer.) x 64 '02) Use integration, the Direct Comparison Test, or the Limit Comparison Test to test the integral for convergence. If more than one method applies, use whatever method you prefer. 116 J' dt 0 + 5in(6t) 1/5 Does converge or diverge? J\" dt 0 M + sin (6t) (:3 Converges {:3 Diverges Use integration, the Direct Comparison Test, or the Limit Comparison Test to test the integral for convergence. If more than one method applies, use whatever method you prefer. oo dx 1x5+2 Choose the correct choice below. 00 00 _ I I I dx I 1 1 I I I 1/(x5 + 2) 1 I i_': A. By the Limit Comparison Test, 5 diverges because 5 and *5 are continuous on the interval [1, oo), lim 75 = 1, and *5dx diverges. 1 x + 2 x + 2 x xmo 1/x , x 00 DO . _ _ dx _ 1 1 _ _ 1 1 1 _ 1in B. By the Direct Comparison Method, 5 diverges because 5 and *5 are continuous on the Interval [1, co), 0 s S *5, and isdx diverges. 1 :1 +2 x +2 x x + 2 x 1 x 1:; c, The integral cannot be evaluated using integration, so the integral diverges. D0 D0 dx 1 1 1 1 1 1] D. By the Direct Comparison Method, I 5 converges because 5 and *5 are continuous on the interval [1, 00), 0s 5*5 on [1, co), and If5dx converges. 1 )1 +2 x +2 x x + 2 x 1 x Use integration, the Direct Comparison Test, or the Limit Comparison Test to test the integral for convergence. If more than one method applies, use whatever method you prefer. Does dx converge or diverge? Taixg+5 1 X8 C:- Diverge C3 Converge