The Legendre polynomials, $Pn(x),$ are a system of orthogonal polynomials discovered in $1782$ by French mathematician Adrien$-$Marie Legendre. $Pn(x)$ is given by Bonnet's recurrence relation

$P_n(x)=\frac{2n-1}{n}x{P}_{n-1}(x)-\frac{n-1}{n}{P}_{n-2}(x)$

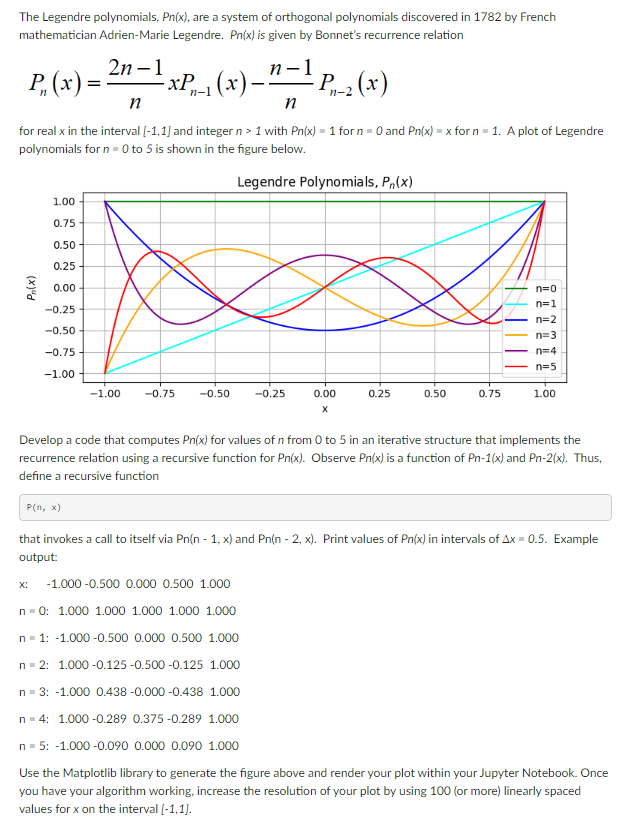
for real $x$ in the interval $-1,1$ and integer $n>1$ with $Pn(x)=1$ for $n=0$ and $Pn(x)=x$ for $n=1.$ A plot of Legendre polynomials for $n=0$ to $5$ is shown in the figure below.

Develop a code that computes $Pn(x)$ for values of $n$ from $0$ to $5$ in an iterative structure that implements the recurrence relation using a recursive function for $P_n(x).$ Observe $P_n(x)$ is a function of $P_{n-1}(x)$ and $P_n-2(x).$ Thus, define a recursive function

that invokes a call to itself via $Pn(n-1,x)$ and $Pn(n-2,x).$ Print values of $Pn(x)$ in intervals of $x=0\mathrm{.}5.$ Example output:

$x$:$,-1\mathrm{.}000,-0\mathrm{.}500,0\mathrm{.}000,0\mathrm{.}500,1\mathrm{.}000$

$n=0$:$,1\mathrm{.}000,1\mathrm{.}000,1\mathrm{.}000,1\mathrm{.}000,1\mathrm{.}000$

$n=1$:$,-1\mathrm{.}000,-0\mathrm{.}500,0\mathrm{.}000,0\mathrm{.}500,1\mathrm{.}000$

$n=2$:$,1\mathrm{.}000,-0\mathrm{.}125,-0\mathrm{.}500,-0\mathrm{.}125,1\mathrm{.}000$

$n=3$:$,-1\mathrm{.}000,0\mathrm{.}438,-0\mathrm{.}000,-0\mathrm{.}438,1\mathrm{.}000$

$n=4$:$,1\mathrm{.}000,-0\mathrm{.}289,0\mathrm{.}375,-0\mathrm{.}289,1\mathrm{.}000$

$n=5$:$,-1\mathrm{.}000,-0\mathrm{.}090,0\mathrm{.}000,0\mathrm{.}090,1\mathrm{.}000$

Use the Matplotlib library to generate the figure above and render your plot within your Jupyter Notebook. Once you have your algorithm working, increase the resolution of your plot by using $100($or more$)$ linearly spaced values for $x$ on the interval $-1,1.$

"code with python"