The objective is to minimize cost while ensuring $73,000$ capacitors and meeting supplier limits$.$ The optimal solution: B $=17,000,$ A $=48,000,$ L $=8,000.$ Total cost: $$345,400.$The linear program minimizes cost for $73,000$ capacitors, allocating $17,000$ from Boston, $48,000$ from Able, and $8,000$ from Lyshenko. This meets supplier limits$,$ yielding a total cost of $$345,400$ for Gulf Coast Electronics. If Cabinetmaker $1$ has additional hours available, would the optimal solution change? If required, round your answers to three decimal places. If your answer is zero, enter $"0".$ Explain.

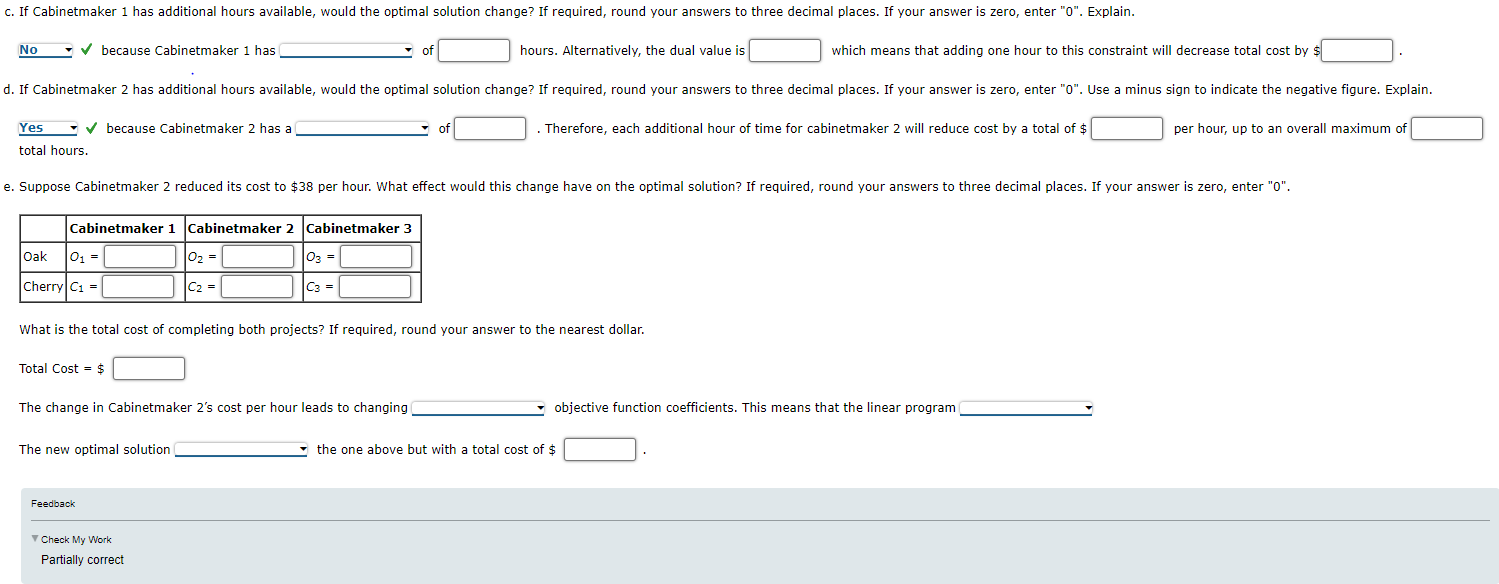
No

because Cabinetmaker $1$ has

of fill in the blank $33$

hours. Alternatively, the dual value is fill in the blank $34$

which means that adding one hour to this constraint will decrease total cost by $fill in the blank $35$

$.$

If Cabinetmaker $2$ has additional hours available, would the optimal solution change? If required, round your answers to three decimal places. If your answer is zero, enter $"0".$ Use a minus sign to indicate the negative figure. Explain.

Yes

because Cabinetmaker $2$ has a

of fill in the blank $38$

$.$ Therefore, each additional hour of time for cabinetmaker $2$ will reduce cost by a total of $ fill in the blank $39$

per hour, up to an overall maximum of fill in the blank $40$

total hours.

Suppose Cabinetmaker $2$ reduced its cost to $$38$ per hour. What effect would this change have on the optimal solution? If required, round your answers to three decimal places. If your answer is zero, enter $"0".$

Cabinetmaker $1$ Cabinetmaker $2$ Cabinetmaker $3$

Oak O$1=$ fill in the blank $41$

O$2=$ fill in the blank $42$

O$3=$ fill in the blank $43$

Cherry C$1=$ fill in the blank $44$

C$2=$ fill in the blank $45$

C$3=$ fill in the blank $46$

What is the total cost of completing both projects? If required, round your answer to the nearest dollar.

Total Cost $=$ $ fill in the blank $47$

The change in Cabinetmaker $2$s cost per hour leads to changing

objective function coefficients. This means that the linear program

The new optimal solution

the one above but with a total cost of $ fill in the blank $51$

$.$c$.$ If Cabinetmaker $1$ has additional hours available, would the optimal solution change? If required, round your answers to three decimal places. If your answer is zero, enter $"0".$ Explain.

$$ because Cabinetmaker $1$ has

of

hours. Alternatively, the dual value is

which means that adding one hour to this constraint will decrease total cost by $

$$ because Cabinetmaker $2$ has a

of

$.$ Therefore, each additional hour of time for cabinetmaker $2$ will reduce cost by a total of $

per hour, up to an overall maximum of

total hours.

What is the total cost of completing both projects? If required, round your answer to the nearest dollar.

Total Cost $=$$

The change in Cabinetmaker $2\text{'}$s cost per hour leads to changing

objective function coefficients. This means that the linear program

The new optimal solution

the one above but with a total cost of $