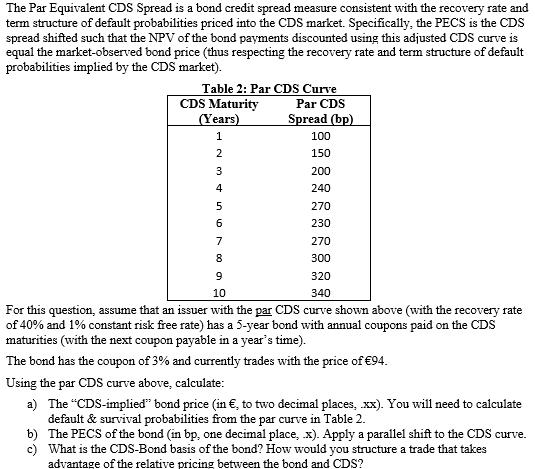
The Par Equivalent CDS Spread is a bond credit spread measure consistent with the recovery rate and term structure of default probabilities priced into the CDS market. Specifically, the PECS is the CDS spread shifted such that the NPV of the bond payments discounted using this adjusted CDS curve is equal the market-observed bond price (thus respecting the recovery rate and term structure of default probabilities implied by the CDS market). Table 2: Par CDS Curve CDS Maturity (Years) 1 684 WN 2 3 4 5 6 7 9 Par CDS Spread (bp) 100 150 200 240 270 230 270 300 320 340 10 For this question, assume that an issuer with the par CDS curve shown above (with the recovery rate of 40% and 1% constant risk free rate) has a 5-year bond with annual coupons paid on the CDS maturities (with the next coupon payable in a year's time). The bond has the coupon of 3% and currently trades with the price of 94. Using the par CDS curve above, calculate: a) The "CDS-implied" bond price (in , to two decimal places, xx). You will need to calculate default & survival probabilities from the par curve in Table 2. b) The PECS of the bond (in bp, one decimal place, .x). Apply a parallel shift to the CDS curve. What is the CDS-Bond basis of the bond? How would you structure a trade that takes advantage of the relative pricing between the bond and CDS? c) The Par Equivalent CDS Spread is a bond credit spread measure consistent with the recovery rate and term structure of default probabilities priced into the CDS market. Specifically, the PECS is the CDS spread shifted such that the NPV of the bond payments discounted using this adjusted CDS curve is equal the market-observed bond price (thus respecting the recovery rate and term structure of default probabilities implied by the CDS market). Table 2: Par CDS Curve CDS Maturity (Years) 1 684 WN 2 3 4 5 6 7 9 Par CDS Spread (bp) 100 150 200 240 270 230 270 300 320 340 10 For this question, assume that an issuer with the par CDS curve shown above (with the recovery rate of 40% and 1% constant risk free rate) has a 5-year bond with annual coupons paid on the CDS maturities (with the next coupon payable in a year's time). The bond has the coupon of 3% and currently trades with the price of 94. Using the par CDS curve above, calculate: a) The "CDS-implied" bond price (in , to two decimal places, xx). You will need to calculate default & survival probabilities from the par curve in Table 2. b) The PECS of the bond (in bp, one decimal place, .x). Apply a parallel shift to the CDS curve. What is the CDS-Bond basis of the bond? How would you structure a trade that takes advantage of the relative pricing between the bond and CDS? c)