Question: The path of a particle is modeled by the function f ( x ) = 1/20 x 2 + 4 x + 7 where f
The path of a particle is modeled by the function
- f(x) = 1/20x2 + 4x + 7
where f(x) is the height (in feet) of the particle and x is the horizontal distance (in feet) from where the particle started moving
a. What is the maximum height (in ft) of the particle?
b. Which number determines the height at which the particle started moving?
c. Does changing this value change the coordinates of the maximum height of the particle? select correct answer.
- Yes, changing this value results in a vertical shift of the graph, so the maximum height changes.
- Yes, changing this value results in both a vertical and a horizontal shift of the graph, so the maximum height changes.
- No, changing this value results in a horizontal shift of the graph, so the maximum height does not change
- No, changing this value does not shift the graph, so the maximum height does not change.
2. For each part, write a cubic function of the form f(x) = (x k)q(x) + r whose graph has the specified characteristics. (There are many correct answers.)
a. passes through the point (5, 8) and rises to the right f(x) =
b. passes through the point (6, 4) and falls to the right
f(x) =
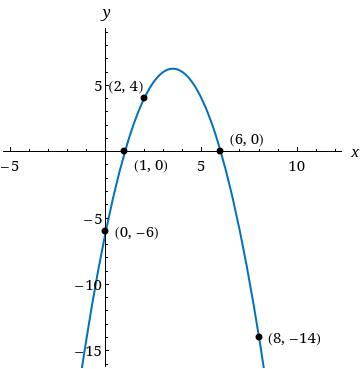
3. Write the standard form of the equation of the parabola shown below. (Let x be the independent variable and y be the dependent variable.)
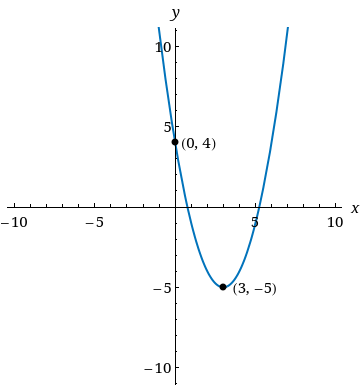
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


