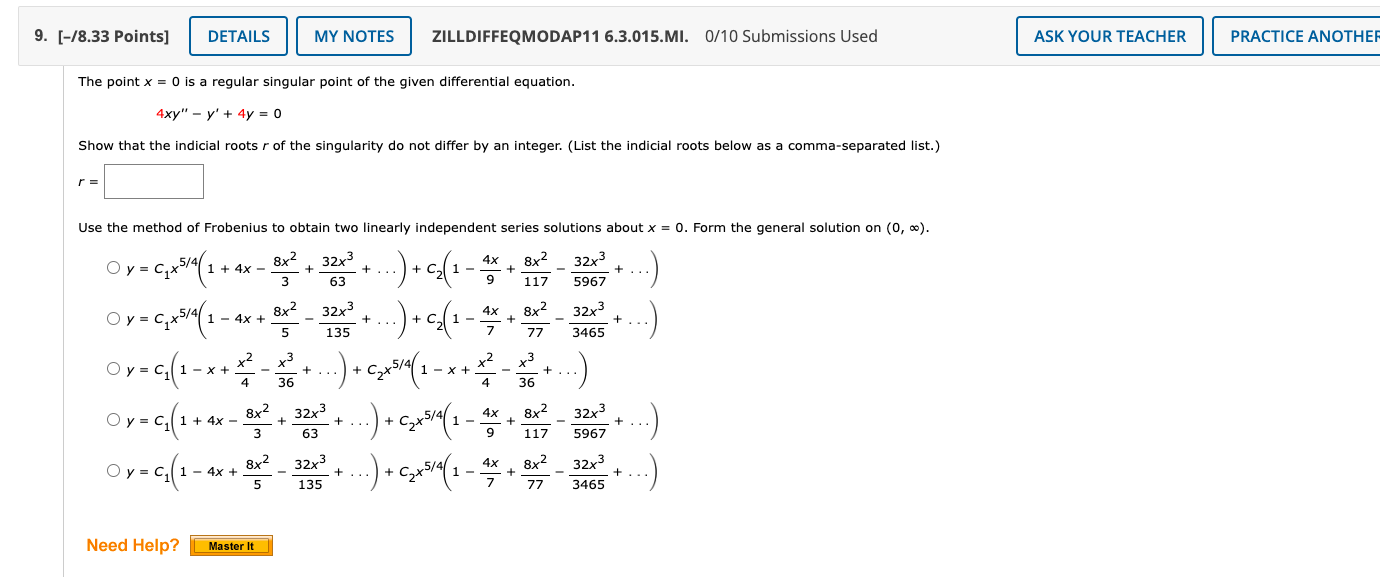
The point x$=0$ is a regular singular point of the given differential equation.

$4$xy$^(\text{'}\text{'})-$y$^(\text{'})+4$y$=0$

Show that the indicial roots r of the singularity do not differ by an integer. $($List the indicial roots below as a comma$-$separated list.$)$

r$=$

Use the method of Frobenius to obtain two linearly independent series solutions about x$=00,\backslash$infty y$=$C$\_(1)$x$^((5)/(4))(1+4$x$-(8$x$^(2))/(3)+(32$x$^(3))/(63)+$dots$)+$C$\_(2)(1-(4$x$)/(9)+(8$x$^(2))/(117)-(32$x$^(3))/(5967)+$dots$)$

y$=$C$\_(1)$x$^((5)/(4))(1-4$x$+(8$x$^(2))/(5)-(32$x$^(3))/(135)+$dots$)+$C$\_(2)(1-(4$x$)/(7)+(8$x$^(2))/(77)-(32$x$^(3))/(3465)+$dots$)$

y$=$C$\_(1)(1-$x$+($x$^(2))/(4)-($x$^(3))/(36)+$dots$)+$C$\_(2)$x$^((5)/(4))(1-$x$+($x$^(2))/(4)-($x$^(3))/(36)+$dots$)$

y$=$C$\_(1)(1+4$x$-(8$x$^(2))/(3)+(32$x$^(3))/(63)+$dots$)+$C$\_(2)$x$^((5)/(4))(1-(4$x$)/(9)+(8$x$^(2))/(117)-(32$x$^(3))/(5967)+$dots$)$

y$=$C$\_(1)(1-4$x$+(8$x$^(2))/(5)-(32$x$^(3))/(135)+$dots$)+$C$\_(2)$x$^((5)/(4))(1-(4$x$)/(7)+(8$x$^(2))/(77)-(32$x$^(3))/(3465)+$dots$)$

Need Help?