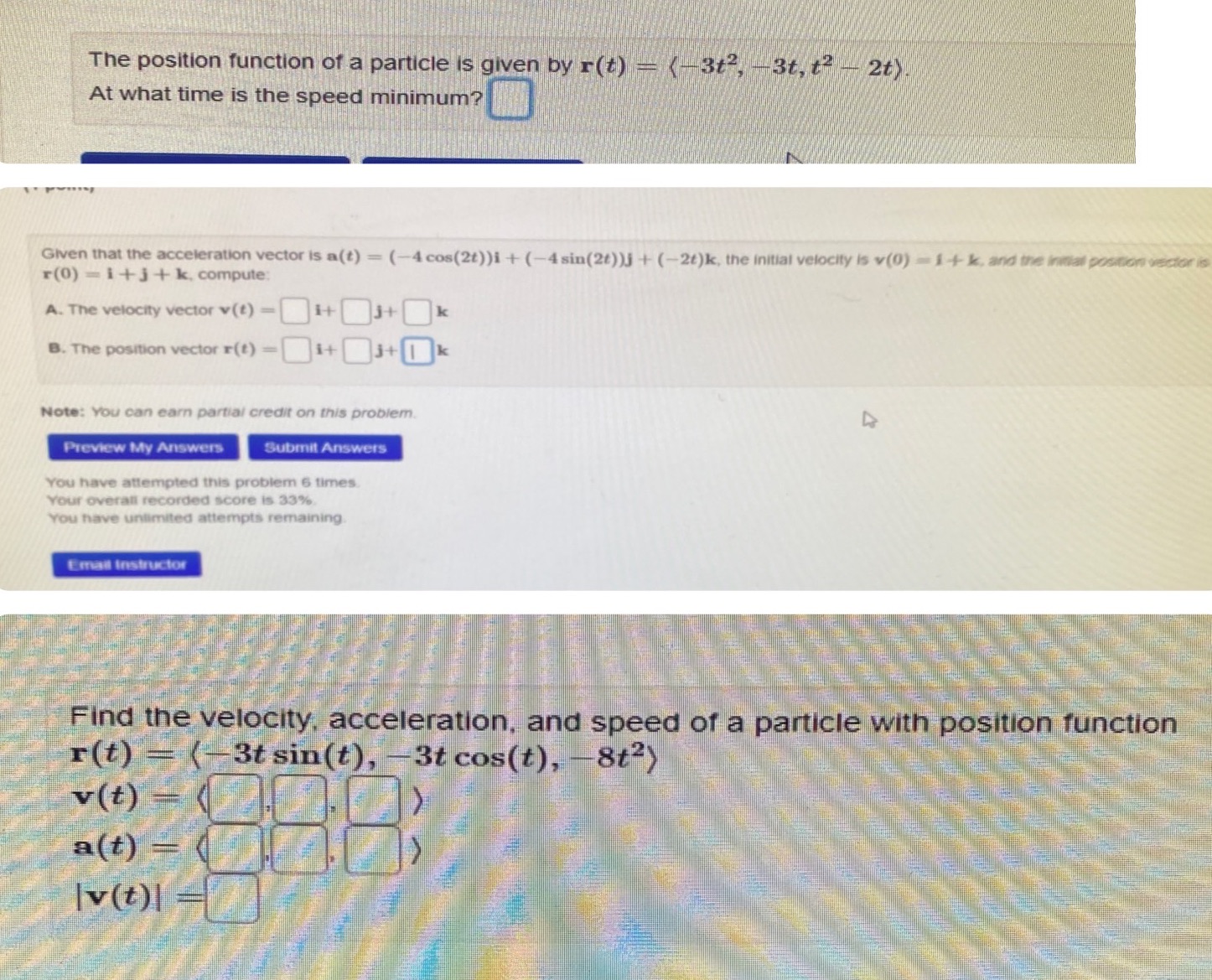
The position function of a particle is given by r(t) = (-3t2, -3t, t2 2t). At what time is the speed minimum? Given that the acceleration vector is a(t) = (-4 cos(2t))i + (-4 sin(2t))j + (-2t)k, the initial velocity is v(0)=1+k, and the initial position vector is r(0) i+j+k, compute: A. The velocity vector v(t) = + B. The position vector x(t) = i+ 3+ k 3+k Note: You can earn partial credit on this problem. Preview My Answers Submit Answers You have attempted this problem 6 times. Your overall recorded score is 33%. You have unlimited attempts remaining. Email Instructor Find the velocity, acceleration, and speed of a particle with position function r(t)=(-3t sin(t), -3t cos(t), -8t2) v(t) = a(t) = |v(t)|