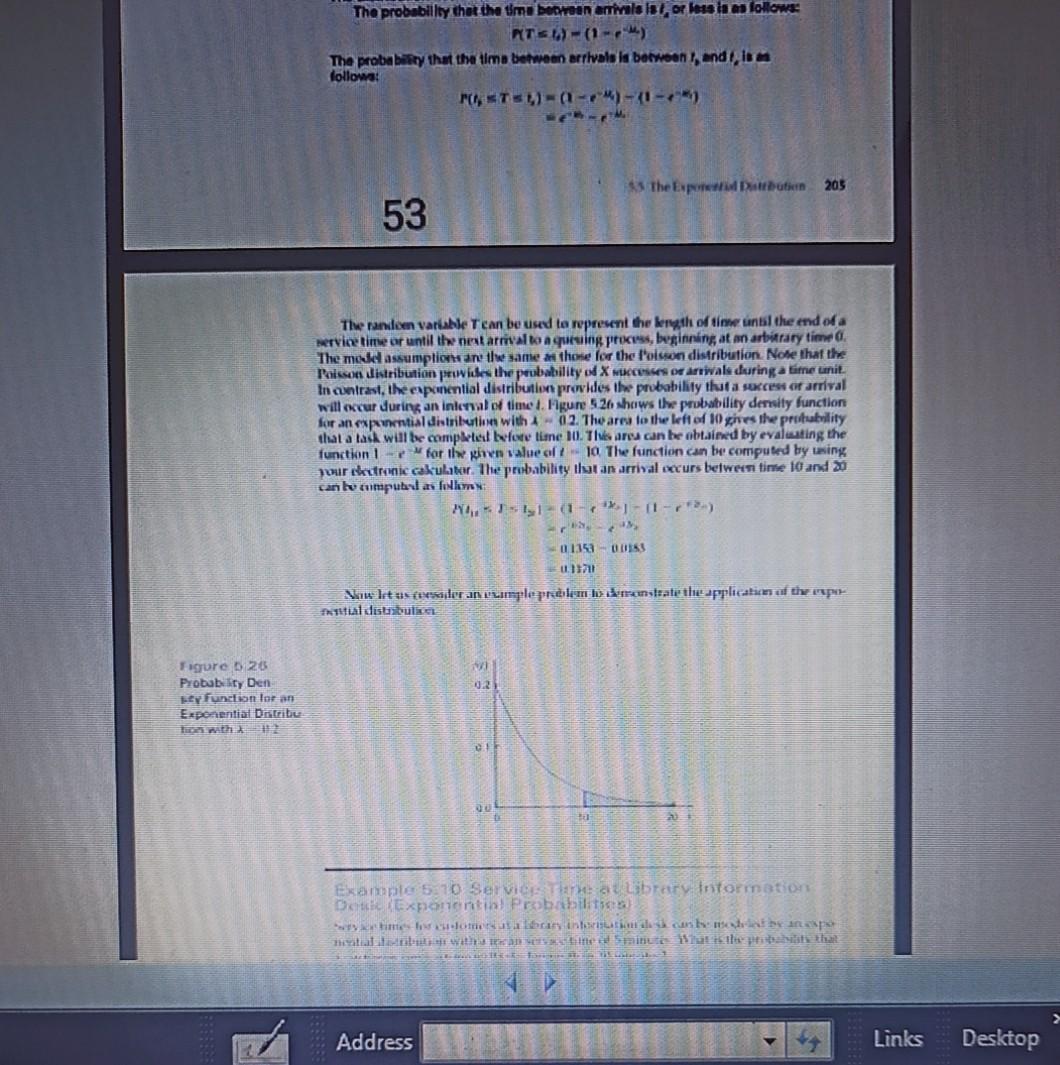
The probability that the time between arrivals ist, or less is as follows: RT) - (1) The probably that the time between arrivals in between I, and I, ia follows: PASTS)-(-)-1= The Experte Dettbutin 205 53 The rand variable T can be used to represent the length of time until the end of a service time or until the next arrivato a queuing process, beginning at an arbitrary time The model I assumplio and the same as there for the l'oluwe distribution. Note that the Poisson distribution prwis the probability of X secusses or anwale during a time unit. In contrast, the exponential distribution provides the probability thut a sexcent et arrival will occur during an interval of time t. Figure 526 shows the probability dernity function for an pwential distributive with 4 - 02. The area to the left of 10 gives the protability that a task will be complet before lime O. TI aru can be obtained by evaluating the function for the phen alue of 10 The function can be computed by using pour ectronic cakulator. The probability that an arrival occurs betwersi time 10 and 20 can lo zumpur as folkem 4.-15151- (1-1-1-2) 0135300SS 1.11701 Vitus (esider av ulimlerdem munstrate the application of the map xtual distaculi w 02 Figure 620 Probability Den ty function lor an Exponential Distribe Ton with UEF 0 ta Example 510 Services are au Library Information Dette exponentia Probabilities times ombrary in the anapo metallic minutes alpint that Address Links Desktop The probability that the time between arrivals ist, or less is as follows: RT) - (1) The probably that the time between arrivals in between I, and I, ia follows: PASTS)-(-)-1= The Experte Dettbutin 205 53 The rand variable T can be used to represent the length of time until the end of a service time or until the next arrivato a queuing process, beginning at an arbitrary time The model I assumplio and the same as there for the l'oluwe distribution. Note that the Poisson distribution prwis the probability of X secusses or anwale during a time unit. In contrast, the exponential distribution provides the probability thut a sexcent et arrival will occur during an interval of time t. Figure 526 shows the probability dernity function for an pwential distributive with 4 - 02. The area to the left of 10 gives the protability that a task will be complet before lime O. TI aru can be obtained by evaluating the function for the phen alue of 10 The function can be computed by using pour ectronic cakulator. The probability that an arrival occurs betwersi time 10 and 20 can lo zumpur as folkem 4.-15151- (1-1-1-2) 0135300SS 1.11701 Vitus (esider av ulimlerdem munstrate the application of the map xtual distaculi w 02 Figure 620 Probability Den ty function lor an Exponential Distribe Ton with UEF 0 ta Example 510 Services are au Library Information Dette exponentia Probabilities times ombrary in the anapo metallic minutes alpint that Address Links Desktop