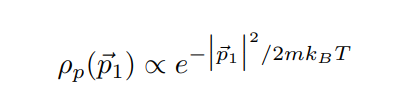
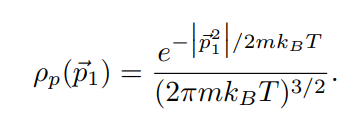
The problem is below:

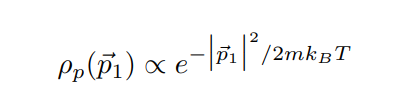
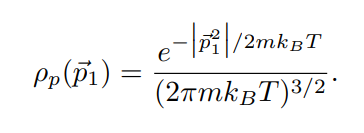
In lecture we will derive the Maxwell distribution of speeds from the canonical ensemble, 3/2 m p (v ) = Arve-mul / kBT 2TKBT (3) where p(v) du is defined as the probability of finding the speed of a particle within some infinitessimal range du of the speed v. Note that this distribution is normalized, fop(v)du = 1. The first few sub-parts of this problem will be laying the groundwork for this result. We assume that we have a "kinetic-plus-potential" Hamiltonian, N p; 12 H = + V({xi}). 2m i=12 Pp(P1) xe P1 /2mkBT2 2mkB e P1 Pp( P1) (2mmkBT) 3/2A very useful skill for Part III of this course will be to change variables in probability distributions or densities. The main rule is that the density times the differential in one set of variables should equal the density times the differential in the other set of variables. If we want to convert between momentum and velocity, for example, we want to satisfy Pp(P1)d' p1 = Pu(v)d35. We can also define the velocity vector 7 by its magnitude v and the spherical angles 0 and y so 835 = 12 du d cos 0 dy. (b) Starting with the result from (a), show that these manipulations do indeed reproduce the Maxwell speed distribution given in Eq. 3. Hint (highlight to reveal): [An intermediate result should be pu(vi) = mopp(mov) ] (c) Show that the rms-speed Urms = (v2) for this distribution matches what we expect from equipartition. [ Supplementary Part (Not for Credit): Also find the expected speed (v) and the speed that occurs with maximum probability Vmax. These three measures should be near each other but different.] [ Supplementary Part (Not for Credit): Graph the distribution and identify Vrms, (v), and Vmax.] Consider a quadratic term in the Hamiltonian in some variable q, Hq-term (q) = C(q - qo)2, where " and go are some constants. Following a similar logic to part (a), we can argue that the probability distribution in q is given by p(q) x e-BC(9-90)2. (d) Find (q), q, and (Hq-term). Commentary: Holy blap! It's equipartition! Finally, suppose we have an ideal gas with particles of mass m in a very tall box (so we can approximate the height as effectively infinite) of cross-sectional area A and subjected to gravity. This adds a gravitational potential energy term to the Hamiltonian, N Hype = > mgzi, where zi is the height of the i-th particle and z = 0 at the base of the box. Assume no other part of the Hamiltonian depends on the particle heights zi. Let the box be in thermal equilibrium with a reservoir of temperature T. (e) Find the normalized probability distribution p( z1) and the expectation value of height (21) for one particle. At what height is the probability of finding a particle a factor of 2 smaller than the probability of finding it at ground level? Commentary: This has been yet another derivation of the law of atmospheres