The Problem

The programming problem in this to find a path from the entry cell (upper left corner) to the exit cell (lower right corner) of a rectangular maze (labyrinth).

The maze is a grid of cells. Each cell is bordered by 4 walls. Some of these walls are passable to the neighboring cell. The border line of the whole maze that is, the perimeter of the rectangle is not passable. You may consider the external walls of the entry as passable one-way in and the external walls of the exit are passable one-way out, though these assumptions are irrelevant to the solution of the programming problem. The program

obtains input to build the a maze; input supplied by an external file

finds a path through a maze if such a path exists

displays the solution (or one of the solutions), that is a path traversing the maze; the display shows all the locations of the cells along the path on the console; the cells listed from entry to exit

determines the farthest cell on an attempted path in the case the traversal failed and displays the path leading to the max distance cell

creates a graphical representation of the solution

There are figures given in an attached file Figures.doc that illustrate the requirements specified in the Problem description.

Analysis and Design

The focus of this project is a class named LinkedMaze that represents a rectangular maze. The maze consist of a two-dimensional array of cell objects, instances of the Cell class. Each cell knows which ones of the four neighbors are accessible from it. A cell can be viewed at as a super-node with five links rather than one (or two). There is a link for each of the directions of north, east, south and west. For an impassable wall the link is null, for a passable wall the link is the neighbor cell in the given direction. The cells maintain yet another link called backLink which points to the predecessor cell on a potential path. In addition to the links a cell has two int type fields to store the indices of the location it takes in the two dimensional array and a boolean field visited which takes true when the cell has been visited during the path finder algorithm. You will have to implement the Queue class based on a circular array which will serve as the main tool for the algorithm searching for the path, and a class Applications to test your program and to run it for several maze applications.

2. Searching for a path

The entry location or starting cell is by definition the upper left corner of the grid, the exit or finish location is the lower right corner. To search for a path from start to finish we use the so called breadth-first algorithm. The logic of this algorithm is quite simple and is described by the following pseudo-code.

Mark the entry cell visited and enqueue

Repeat:

dequeue

if exit is a neighbor of the current (dequeued) cell, stop the algorithm and build the output for the successful search

otherwise check the four directional links of the current cell

for each non-null and non-visited link mark the link visited, add it to the queue and assign the added links backlink the current cell

Stop the algorithm if the queue is empty and build the output for the failed search

The pseudo-code above must be refined in order to deal with max distance cell. If row is the row index and column is the column index of a cell in the two dimensional array, the distance of that cell from the entry is measured by row + column (sometimes this distance is referred to as the Manhattan distance). A variable maxDistance must store the largest distance value found this far and another variable maxCell referes to the cell where the maxDistance has been attained. Every time an east link or a south link is added to the queue, the distance of the link is to be compared to the current maxDistance. In case of a greater link distance, the maxDistance variable is updated and link is the new value for maxCell. Note that north and west links never increase the distance thus they are ignored.

A partial specifications for the classes are given as follows.

Cell

row, column int type to store the location coordinates of the Cell in the grid (array)

nLink, eLink, sLink, wLink, backLink Cell references; a directional link, like nLink to north is null if the corresponding wall (like north wall) of this cell is not passable

visited boolean; marks the cell with true if it has been enqueued; value never changed back to false later

Cell( ) constructor, takes two int parameters for the array coordinates, initializes the coordinates. Note that at Cell instantiation all the links keep the default null value and visited stays false.

linked( ) static utility method, returns boolean; takes two cells for parameter and determines if one is an accessible neighbor of the other, that is if one is a directional link of the other

toString( ) -- returns a string that shows the field values row and column

sum( ) convenience method returns row+column; helps to maximize distance

Queue

Fields (private)

manyItems, front, rear (int types)

theQueue (a circular array of cell objects)

Constructor (takes a parameter for array size and instantiates the array (NOT the array elements))

LinkedMaze

The class needs the following fields:

pathfinder; a Queue reference

entry, exit, maxCell; Cell references

cells; a Cell[][] array

length, width, maxDistance; int type variables to store the dimensions of the cells array and the maximum distance from the entry cell

The behavior of LinkedMaze is suggested as follows:

LinkedMaze ( ) -- constructor; takes the grid dimensions and a Queue reference for parameters to initialize those fields. Instantiates the cells array to the given dimensions. Populates the array with Cell objects. Assigns entry the cells[0][0] element and exit the lower right corner element of the array

connectMaze( ) void, takes two Scanner objects to read the files characterizing the north-south walls, and the other file having the east-west walls. Runs a nested pair of for loops to assign correct values to the directional links of each cell

findPath( ) runs the search algorithm; see the pseudo code and additional hints above; returns boolean

reversePath ( ) takes a cell for parameter and returns a cell. Given a cell current on a path, the backLinks create a linked list such that current is the head and entry is the tail. The method reverses the links and makes entry the head and current the tail. Note that the reverse must not be called if additional cell operations will be needed along the path elements, only when it comes to display the path.

displayPath ( ) prints the coordinates of the cells along a path, starting at the entry cell (before this method, must call reversePath( ))

Implementation, Testing and Applications

You must use the classes, class names, data structures and functionalities as described in the Design

Additional methods and/or fields are allowed, but if you choose so, must give very thorough documentation to help the grader to identify the functionalities

You must include the full specification of the LinkedMaze class. Specification of other classes and methods is optional

Make sure that data structure classes follow the traditional usage of field and method names

Using generic type(s0 is not required

This class drives all the maze applications.

The maze configuration

Solicit the input file names on the console is input directly in the code. The attached Figures.doc file shows maze examples and associated input files.

The grid dimensions are contained in the first row of the eastWest file. The dimensions must read first, before the actual wall information reading is processed

The eastWest file contains the east-west wall information listed row-by-row.

Notice that only the east directions are listed, since a passable east wall is at the same time a passable west wall for the next cell to the right. For the same reason the northSouth file gives a listing on the south direction only.

Instantiate Scanner objects to read the files and read the dimension first.

Knowing the dimensions instantiate the Queue object pathfinder. Meditate a bit about a good choice for the length of the queue (not too long still making the ensureCapacity call unlikely)

Having the dimensions and pathfinder obtained, instantiate a LinkedMaze object maze

Call the connectMaze( ) method (you have the Scanners at hand for parameter)

Call the findPath( ) method and store the return value in a boolean variable flag

Call the displayPath( ) method; depending on the flag value display the path traversing the entire maze, or just a partial path running to the farthest cell found and print out the maximum distance

eastWest.txt

10 10 0 0 0 1 0 0 0 0 0 1 0 0 1 1 1 0 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 1 0 0 0 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 1 0 0 1 1 1 0 1 0 1 0 1 0 0 1 0 0 1 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 0 1

northSouth.txt

1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 1 0 1 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 0 0 1 0 1 1 0 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1

Figures.doc

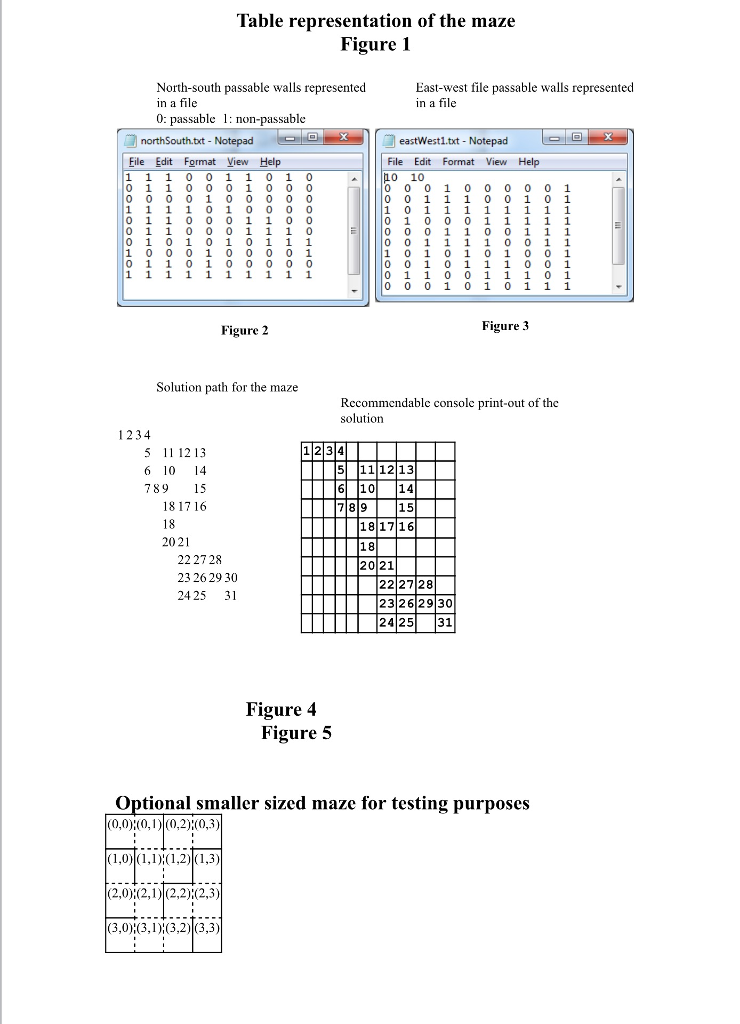
Table representation of the maze Figure 1 North-south passable walls represented East-west file passable walls represented in a file n a file 0: passable non-passable X eastWest 1.tot-Notepad northSouth.txt Notepad File Edit Format View Help File Edit Format View Help po 10 0 0 0 1 0 0 0 0 0 1 0 1 1 1 0 1 0 1 0 1 1 0 0 1 1 0 0 1 0 1 0 0 1 1 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 0 1 0 1 0 1 1 Figure 3 Figure 2 Solution path for the maze Recommendable console print-out of the solution 1234 2 13 5 11 12 13 789 15 6| 10| |14 18 1716 181716 202 222728 2021 23 2629 30 22 27 28 24.25 31 23 26 29 30 2425 31 Figure 4 Figure 5 Optional smaller sized maze for testing purposes (0,0) (0,1) (0,2) (0,3) (1,0) (1,1) (1,2) (1,3) 2,0) (2,1) (2,2) (2,3 3,0) (3,1) (3,2) (3,3 Table representation of the maze Figure 1 North-south passable walls represented East-west file passable walls represented in a file n a file 0: passable non-passable X eastWest 1.tot-Notepad northSouth.txt Notepad File Edit Format View Help File Edit Format View Help po 10 0 0 0 1 0 0 0 0 0 1 0 1 1 1 0 1 0 1 0 1 1 0 0 1 1 0 0 1 0 1 0 0 1 1 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 0 1 0 1 0 1 1 Figure 3 Figure 2 Solution path for the maze Recommendable console print-out of the solution 1234 2 13 5 11 12 13 789 15 6| 10| |14 18 1716 181716 202 222728 2021 23 2629 30 22 27 28 24.25 31 23 26 29 30 2425 31 Figure 4 Figure 5 Optional smaller sized maze for testing purposes (0,0) (0,1) (0,2) (0,3) (1,0) (1,1) (1,2) (1,3) 2,0) (2,1) (2,2) (2,3 3,0) (3,1) (3,2) (3,3