the python code of this question ~thx!:)

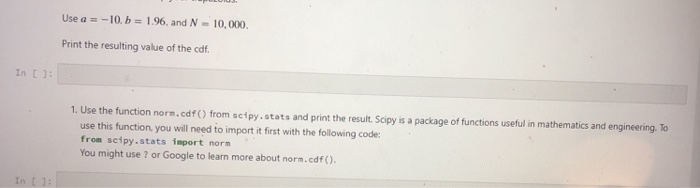
Recall from your statistics or econometrics class that the probability density function (pdf) of a normal distribution with mea given by n u and variance o is f(x) = The corresponding cumulative distribution function (cdf) is Unfortunately, the caf F'(x) does not have numeric integration (ie, a computer) to calculate the value of the cdf at a given point. a closed-form expression: we cannot compute this integral by hand. Instead, we use a technique called accurate numeric integration technique is the trapezoid rule, which One simple but reasonably trapezoid rule approximates the area under a curve g(x) with the area of N trapezoids of is taught in every equal width. Formally. ry introductory calculus course. The call where In this exercise, your task is to calculate the value of the cdf of the standard normal distribution (ie, -: 0 and 2 1) at n. 196 we will do it two ways. First on our own (to practice some list comprehensions) and then, the easy way, using the norm function from scipy. 1. Write your own code. Your goal is to compute the summation that approximates the integral. Use three list comprehensions. First, create and store the points ( a + k, ) at which the pdf is calculated Second. create and store the values (gla + kAx)) of the pdf at each of those points, and Third. create and store the areas (o.Sg1k]+k+1)Ar)of each trapezoid. Fourth sum up your trapazoids * Use a =-10, b-l .96, and N = 10,000. Print the resulting value of the cdf Recall from your statistics or econometrics class that the probability density function (pdf) of a normal distribution with mea given by n u and variance o is f(x) = The corresponding cumulative distribution function (cdf) is Unfortunately, the caf F'(x) does not have numeric integration (ie, a computer) to calculate the value of the cdf at a given point. a closed-form expression: we cannot compute this integral by hand. Instead, we use a technique called accurate numeric integration technique is the trapezoid rule, which One simple but reasonably trapezoid rule approximates the area under a curve g(x) with the area of N trapezoids of is taught in every equal width. Formally. ry introductory calculus course. The call where In this exercise, your task is to calculate the value of the cdf of the standard normal distribution (ie, -: 0 and 2 1) at n. 196 we will do it two ways. First on our own (to practice some list comprehensions) and then, the easy way, using the norm function from scipy. 1. Write your own code. Your goal is to compute the summation that approximates the integral. Use three list comprehensions. First, create and store the points ( a + k, ) at which the pdf is calculated Second. create and store the values (gla + kAx)) of the pdf at each of those points, and Third. create and store the areas (o.Sg1k]+k+1)Ar)of each trapezoid. Fourth sum up your trapazoids * Use a =-10, b-l .96, and N = 10,000. Print the resulting value of the cdf