Question: The question 5. Let X = {y E C'[0, In 2] : y(In 2) = 4} and consider the functional J : X -> R

The question

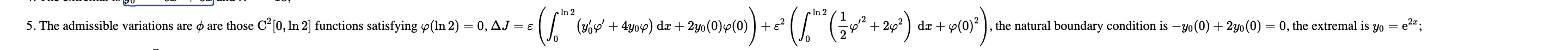
5. Let X = {y E C'[0, In 2] : y(In 2) = 4} and consider the functional J : X -> R defined by In 2 2 dy Jly = + 272 dx da + (y(0) ) 2 + 43(In2) Find, from first principles, an extremum yo E X of J and show that yo is a minimum.5. The admissible variations are o are those C2 [0, In 2] functions satisfying 4 (In 2) = 0, AJ = = ( (uop' + 4yo4) dx + 2yo(0)4(0) ) += (242 + 242 ) dx + 4(0)2 ) , the natural boundary condition is -yo (0) + 2yo(0) = 0, the extremal is yo = e2z

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Information For questions 1 - 2, use the graph of the function below. -10 Question 1 Identify the interval(s) where the function increases. Select all that apply. Not yet answered Select one or more:...

Proccess is key 2 5:5 :5 + 5 . Let F = {:12 E 'R, : f (:12) is strictly increasing} and Consider the following functions: f (:3) = and 6"" + log(x + 2) 9(33) = W G denote the domain of 9(32). (21)...

Problem 4 Let f : R2 -> R. Consider the problem minimize f(x) s.t. X1, X2 2 0 where a = (21, 12) . Suppose that Vf(0) # 0, and of (0) So, of (0) SO Show that 0 cannot be a minimizer for this problem....

Let = {1, 2, 3, 4, 5}. Let a filtration Ft , t = 0, 1, 2, in be given by F0 = {, }, F1 corresponds to the partition P1 = {{1, 2}, {3, 4, 5}}, F2 = P(). Consider a probability measure P on defined by...

Question 4: You repeatedly flip a fair coin and stop as soon as you get tails followed by heads. (All coin flips are mutually independent.) Consider the random variable X = the total number of coin...

I need help solving this mathematical question Question 3 The following sample data represent students scores in two replacement Math exams. Question 5 Let x represents the number of overweight men....

Curve Sketching - Polynomials We're going to do the Curve Sketching Algorithm. f(x) = x5- 5x3+ 4x f' (x ) = 5x - 15x7 + 4 f" (x) = 20x - 30x A: Domain: B: Intercepts: y-int (0,0) x-int (op) (-1, 0),...

Il. Relative Velocity Question Proof/Work/Explanation (1) A person wants to paddle a canoe from point to point, which is directly across a river from point , as shown in the figure above. The water...

The Gamma distributionwith paramters fa,f (x) =Fox -e Ox for allx 2 0. The I function is defined by T (s) = xtte * dx. As usual, the constant - is a normalization constant that gives ffa,, (x) dx =...

Let X 1 , X 2, ..., X 10 be a sample from a N(25, 5 2 ) distribution, independent of the sample Y 1, Y 2, ..., Y 20 coming from a N(0, 10 2 ) distribution. STA2603_2021_Assignment 6.pdf x *Homework...

DCF cost of Equity Estimation what are the advantages of using the DCF model for determining the cost of equity capital? What are the disadvantages? What specific piece of information do you need to...

The alliance between Renault and Nissan is just one example of the cross-border alliances that permeate the global auto industry. Ask your students to identify other alliances between auto companies...

3. What is the relationship between thinking distance and speed?

Sherrod, Inc., reported pretax accounting income of $92 million for 2021. The following information relates to differences between pretax accounting income and taxable income: Income from installment...