The question is shown in the picture

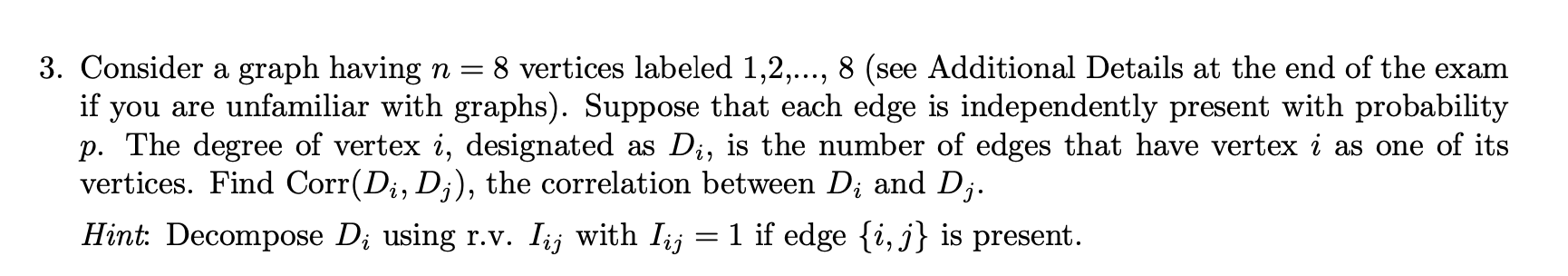
Exercise 2 (3 + (2 + 1) + 4 pts.). Covariance, Correlation, Multivariate Normal Distribution. 1. Is it possible for two random variables X and Y to satisfy E[X] = 1, E[Y] = 2, E[X2] = 3, E[Y2] = 5, and E[XY] = -1? 2. Suppose that X and Y are independent standard normal random variables. Define U = (X + Y) and V = 4 (X - Y). (a) What are the distributions of U and V (give the name of the distribution and the parameters that define these r.v.) (b) Are U, V independent?3. Consider a graph having n = 8 vertices labeled 1,2,..., 8 (see Additional Details at the end of the exam if you are unfamiliar with graphs). Suppose that each edge is independently present with probability p. The degree of vertex i, designated as Di, is the number of edges that have vertex i as one of its vertices. Find Corr(D,;, Di): the correlation between D:- and Dj. Hint: Decompose D,- using r.v. Ii]- with Ii]- = 1 if edge {i, j} is present