The R CODE of loading data packages:

install.packages("astsa")

library(astsa)

par(mfrow=c(3,1)) # plot the data

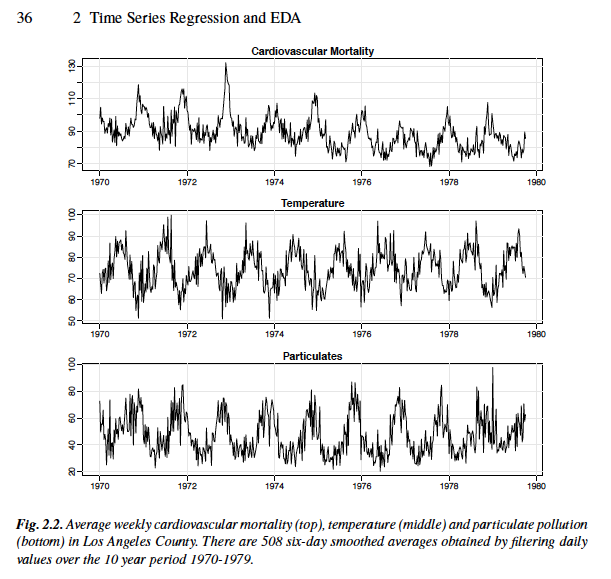
tsplot(cmort, main="Cardiovascular Mortality", ylab="")

tsplot(tempr, main="Temperature", ylab="")

tsplot(part, main="Particulates", ylab="")

dev.new() # open a new graphic device

ts.plot(cmort,tempr,part, col=1:3) # all on same plot (not shown)

legend('topright', legend=c('Mortality', 'Temperature', 'Pollution'),

lty=1, col=1:3)

dev.new()

pairs(cbind(Mortality=cmort, Temperature=tempr, Particulates=part))

temp = tempr-mean(tempr) # center temperature

temp2 = temp^2

trend = time(cmort) # time

fit = lm(cmort~ trend + temp + temp2 + part, na.action=NULL)

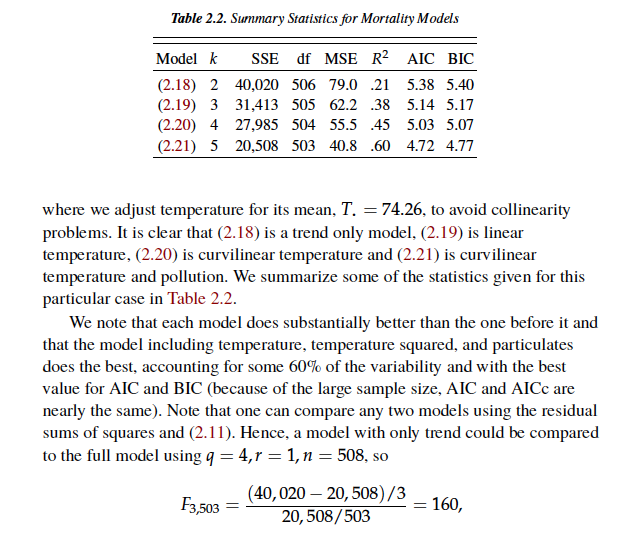
summary(fit) # regression results

summary(aov(fit)) # ANOVA table (compare to next line)

summary(aov(lm(cmort~cbind(trend, temp, temp2, part)))) # Table 2.1

num = length(cmort) # sample size

AIC(fit)um - log(2*pi) # AIC

BIC(fit)um - log(2*pi) # BIC

(AICc = log(sum(resid(fit)^2)um) + (num+5)/(num-5-2)) # AICc

ct ct be the cardiovascular mortality series (ort) discussed in Chapter 2, Example 2.2 and let Xt Ct be the differenced data. Plot x and compare it to the actual data plotted in Figure 2.2. Why does differencing seem reasonable in this case? that an AR(1) is appropriate for x squares) as in Section 3.6. The easiest way to do this is to use sarima from the model. What is t (b) Calculate and plot the sample ACF and PACF of x and using Table 3.1, argue (c) Fit an AR(1) to Xt using maximum likelihood (basically unconditional least he estimate of the whiten (d) Examine the residuals and comment on whether or not you think the residuals are white. ct ct be the cardiovascular mortality series (ort) discussed in Chapter 2, Example 2.2 and let Xt Ct be the differenced data. Plot x and compare it to the actual data plotted in Figure 2.2. Why does differencing seem reasonable in this case? that an AR(1) is appropriate for x squares) as in Section 3.6. The easiest way to do this is to use sarima from the model. What is t (b) Calculate and plot the sample ACF and PACF of x and using Table 3.1, argue (c) Fit an AR(1) to Xt using maximum likelihood (basically unconditional least he estimate of the whiten (d) Examine the residuals and comment on whether or not you think the residuals are white