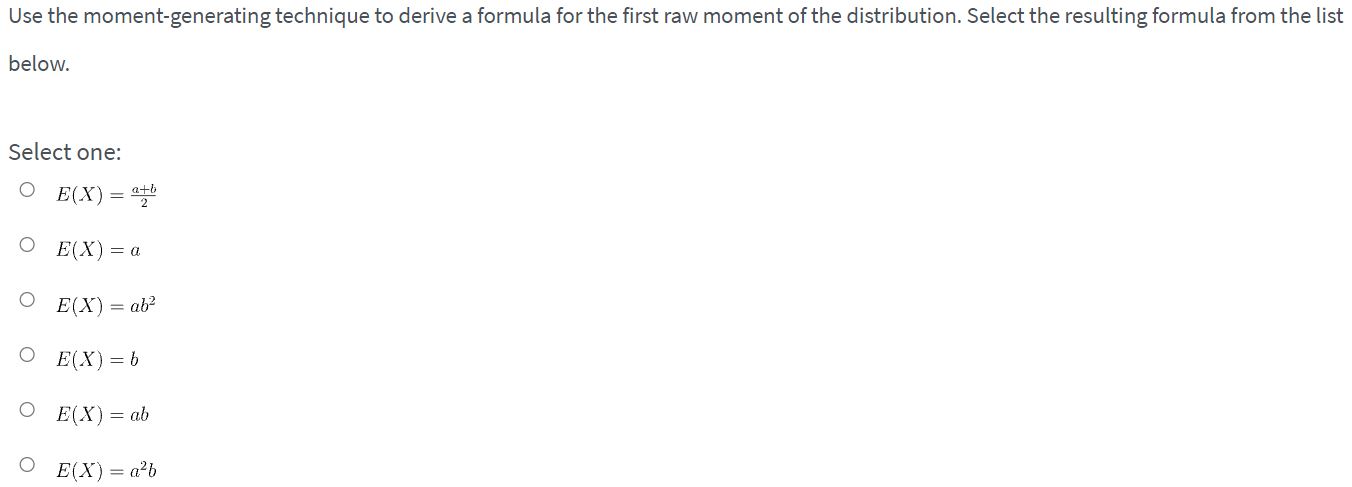
The random variable X has a probability distribution with moment-generating function ofthe following form: M\") = exp(at + 325': . Use the moment-generatingfunction technique to derive the raw moments ofthe distribution specied in the questions below. Then use these raw moments to derive formulas for the distributional characteristics requested. Use the moment-generating technique to derive a formula for the first raw moment of the distribution. Select the resulting formula from the list below. Select one: O E(X) = att O E(X) = a O E(X ) = ab- O E(X) = b O E(X) = ab O E(X) = albUse the moment-generating technique to derive a formula for the second raw moment of the distribution. Select the resulting formula from the list below. Select one: O E( X? ) = a262 O E(X2 ) = 42 O E(X? ) = 62 O E(X? ) = a2 + 62 O E(X? ) = ab2 O E(X2 ) = a2bDetermine the formula for the mean, /x, of the distribution. Select the resulting formula from the list below. Select one: O fr = b O Ha = 62 O He 2 O Hz = a O Hy = a'b O Ha = ab2Determine the formula for the variance, 0: , of the distribution. Select the resulting formula from the list below. Select one: I _ 12 O a\": = :11; O or: = azbz