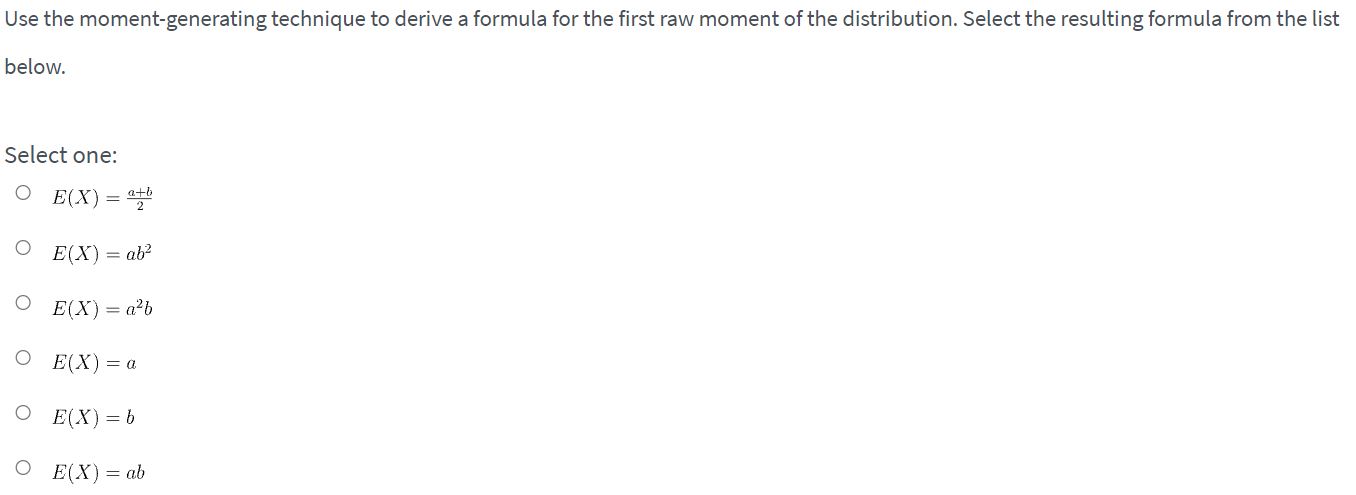
The random variable X has a probability distribution with moment-generating function ofthe following form: MU) = (1 bt]'\". Use the moment-generatingfunction technique to derive the raw moments of the distribution specified in the questions below. Then use these raw moments to derive formulas for the distributional characteristics requested. Use the moment-generating technique to derive a formula for the first raw moment of the distribution. Select the resulting formula from the list below. Select one: O E(X) = ath 2 O E(X) = ab- O E( X ) = ab O E(X ) = a O E(X) = b O E(X) = abUse the moment-generating technique to derive a formula for the second raw moment of the distribution. Select the resulting formula from the list below. Select one: O E ( X? ) = a2b O E(X2 ) = ab O E(X2 ) = a262 - ab2 O E(X? ) = a262 + ab2 O E( X2 ) = ab + a262 - ab2 O E(X? ) = ab-Determine the formula for the mean, \"at, of the distribution. Select the resulting formula from the list below. Select one: Q #2 = I, O aux = \"T\" o M = a O #3 - ab 0 or = azb O \"I = ab: Determine the formula for the variance, or: , of the distribution. Select the resulting formula from the list below. Select one: 0 a2=ab(1b) O or: = (12!?2 0 a2 = Lei-\":3\" O o=ab2 O a=a2b