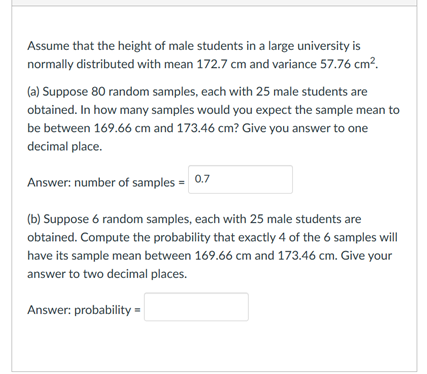
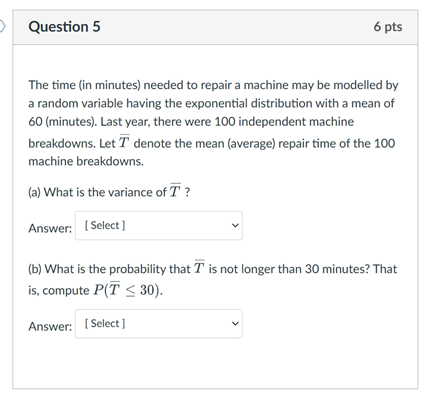
The random variable Y has the Poisson distribution with a mean of 50. {a} What is the variance of Y? Answer: 50 {b} Compute the probability. P(Y > 60). Select the closest answer. Answer: [ 5m\" 1 " [C] Le: Y1 and Y; be two independent observations of Y. What is the variance of {Y1 + Y2]? Answer: variance'. + Y?) - [5eIect] v {ii} Let Y1 and Y2 be two independent ubSEnrat-ions of Y. What is the variance of (1"; Y2)? Answer: variance(Yl Y2) = [53'1\"] \" Suppose the average price of a gallon of unleaded fuel at gas stations across the country is $1.897. Assume that the standard deviation of these prices is $0.15 per gallon. A random sample of 100 gas stations is drawn from parts of the country. Let X denote the average price of a gallon of unleaded fuel at the gas stations in the sample. (a) What is the standard deviation of X ? Answer: [ Select ] (b) What is the probability that X is between $1.90 and $1.92? Answer: [ Select ]a. Question 5 6 D15 The time (in minutes] needed to repair a machine may be modelled by a random variabie having the exponential distribution with a mean of 60 (minutes). Last year. there were 100 independent machine breakdowns. Let ? denote the mean {average} repair time of the 100 machine breakdowns. la! What is the variance of T ? Answer: | 59'9\" I " lb} What is ihe probability that T is not longer than 30 minutes? That is. compute H? E 30}. Answer: ism\" l " Which of the following statements is TRUE? O The binomial distribution with parameters n and p may be approximated by a normal distribution with the same mean and variance, N(np, npq), when both np and nq are at most 5. Here q = 1 - p. O The binomial distribution with parameters n and p may be approximated by a normal distribution with the same mean and variance, N(npq. np ). when both np and nq are at least 5, Here q =1 - p. O The Poisson distribution with parameter u may be approximated by a normal distribution with the same mean and variance, N(J. [). when u is at least 30. O The Poisson distribution with parameter u may be approximated by a normal distribution with the same mean and variance. N(J. p). only when u is at most 30.An instructor for a statistics course collected data on the weight (in grammes) of humming birds. Her sample comprises 225 birds drawn at random from areas all across the country. The students in the statistics course were divided into three groups and assigned to construct a 95% confidence interval estimate for the average weight (in g) of a humming bird using all the information in the data set. The confidence intervals obtained were: Group A: 2.944