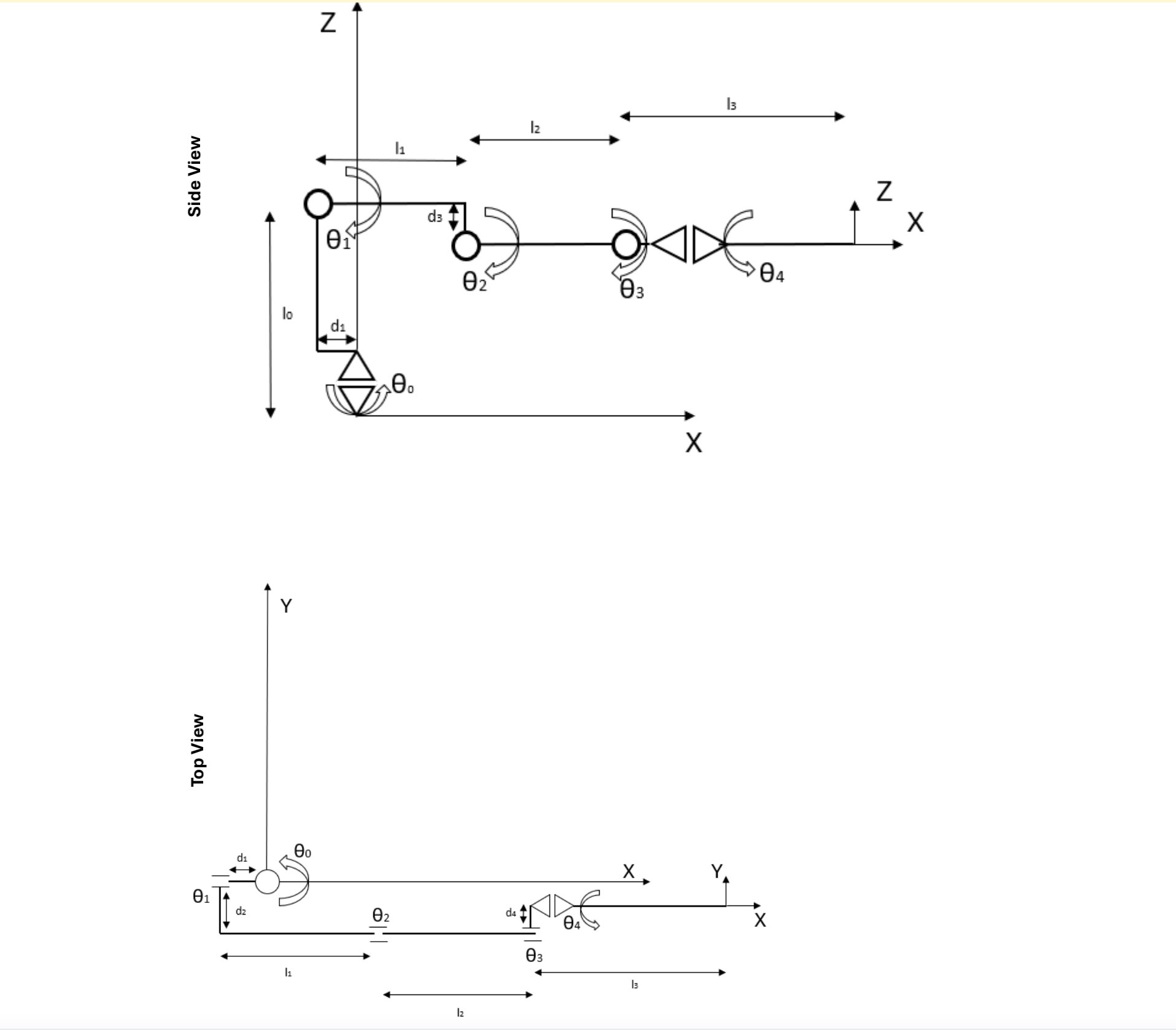
The RobotIn the first examples you are to determine the forward kinematics and a partial inverse kinematics for the following $5$ degree$-$of$-$freedom robot manipulator:$($see the figures$)$The link length are defined as follows:l$0=0\mathrm{.}35$m l$1=0\mathrm{.}25$m l$2=0\mathrm{.}15$m l$3=0\mathrm{.}2$mIn addition there are multiple offsets that represent displacements at the joints.The offsets are d$1=0\mathrm{.}03$m between joint $1$ and joint $2,$ d$2=$ d$3=0\mathrm{.}04$between joint $2$ and joint $3,$ and offset d$4=0\mathrm{.}025$m between joint $4$ and joint$5$ of this robot. The picture above shows the robot in the configuration where alljoint angles are $0.$The offset are defined as follows:d$1=0\mathrm{.}03$m d$2=0\mathrm{.}04$m d$3=0\mathrm{.}04$m d$4=0\mathrm{.}025$mThe simulator will actually show one additional joint $($joint $5)$ correspondingto the opening of the gripper. This, however, is not relevant for the kinematicfunctions$\mathrm{.}1.$ Determine and implement the forward kinematic function for this Robot.Derivation$[30],$Code$[15]$ total$[45]$Here you are supposed to determine the transformation from configurationspace $($joint angles$)$ to the Cartesian location of the tool frame $(\{$T$\})$ inbase frame coordinates $(\{$B$\})$ using Homogeneous transformation. You onlyhave to provide the position. The orientation of the tool frame is not required.$($HINT: What effect does the last joint, $4,$ have on the location of the toolframe $?)$For this part of the assignment you are to hand in a written version of theforward kinematics and your derivation $($either closed form or as a sequenceof transformation matrices$),$ and the code $($homogeneous or trigonometric$)$for the forward kinematic function you implemented.For the implementation you have to write the function fwd kin$()$ inside thefile kin fncs$.$c$.$ This function has the following structure:fwd$\_$kin$($theta$,$ x$)$double theta$[6]$;double x$[3]$;$\{...\}$It gets passed in an array containing the $6$ joint angles theta $($the last anglecorresponds to the gripper and is of no interest here$)$ and should calculate x $,$the $3$ dimensional position of the tool frame $($x$[0]=$ x$,$ x$[1]=$ y$,$ x$[2]=$ z$)\mathrm{.}3.$ Determine a partial inverse kinematic function for the robot and implementit in the simulator. Derivation$[40],$Code$[15]$ total$[55]$In this part of the assignment you are to derive and implement an inversekinematic function for the robot manipulator for a specific orientation ofthe tool frame $($if multiple solutions exist only one is required here$).$ Thisorientation is given by $4=0$ and the requirement that the X$-$axis of thetool frame is parallel to the Z$-$axis of the base frame but in the oppositedirection. In other words, the last link of the manipulator is to point straightdown. $($HINT: To determine this inverse kinematics you should decomposethe problem. You can determine $0$ and $3$ separately and calculate theother joint angles by analyzing the substructure formed by links $1$ and $2($l$1$and l$2).$ This requires moving the wrist frame to joint $3.)$Again you are to hand in a written version of this inverse kinematics andits derivation and the code. The code here should be implemented in thefunction inv kin$().$inv$\_$kin$($x$,$ theta$)$double x$[3]$;double theta$[6]$;$\{...\}$This function gets passed in the location of the tool frame $($x$)$ and has tocompute a corresponding joint angle configuration $($theta$).$ps:the code is not does not matters. I could not develop the math ways to its derivation.

I will upvote it thanks to ur efforts In advance.

And i will $100\%$ report the spam answers.