Question: The simple graphs G_1 = (V, E_1) and G_2 = (V_2, E_2) are isomorphic if there exists a one-to-one and onto function f from V_1

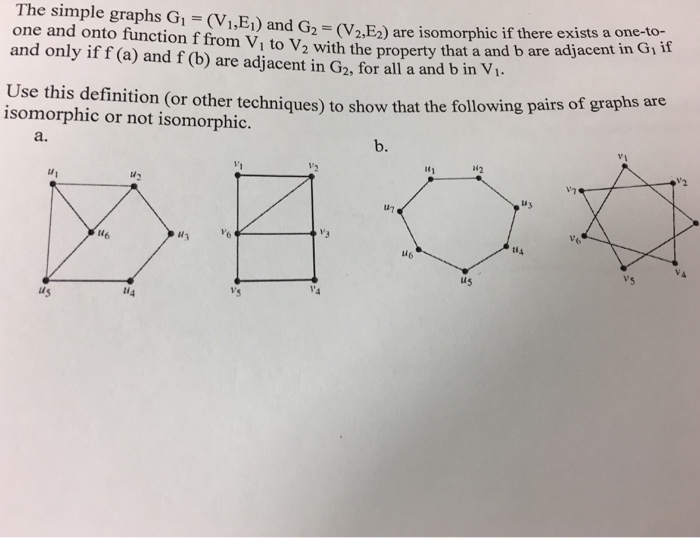
The simple graphs G_1 = (V, E_1) and G_2 = (V_2, E_2) are isomorphic if there exists a one-to-one and onto function f from V_1 to V_2 with the property that a and b are adjacent in G_1, if and only if f(a) and f(b) are adjacent in G_2, for all a and b n V_1. Use this definition (or other techniques) to show that the following pairs of graphs are isomorphic or not isomorphic

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

When a vertex v is connected by an edge to a vertex w, what is the term for the relationship between v and w? Question 1 options: a) v and w are \"adjacent.\" b) v and w are \"incident.\" c) v and w...

Two graphs G_1 = (V_1, E_1) and G_2 = (V_2, E_2), such that V_1 = V_2 = {1, 2, ..., n} are isomorphic if there is a one-one, onto function pi: {1, 2, ..., n} rightarrow {1, 2, ..., n} such that for...

Two graphs G_1 = (V_1, E1) and G_2 = (V_2, E_2) such that V_1 = v_2 = {1, 2, ..., n} are isomorphic if there is a one-one, onto function pi: {1, 2, ..., n} rightarrow (1, 2, ...., n} such that for...

Two graphs G1 = (V1, E1) and G2 = (V2, E2), such that V1 = V2 = {1, 2, , n} are isomorphic if there is a one-one, onto function : {1, 2, , n} {1, 2, , n} such that for every i, j {1, 2, , n} E1 E2...

If we have two graphs G1 = (V1, E1) and G2= (V2, E2) and V1 = {a, b, c}, E1 = {(a, c), (b, c), (a, b)}, V2 = {a, b, c}, E2 = { (c, a) , (c, b), (a, b) }. Which statement below is not true? Question...

Two graphs G_1 = (V_1, E_1) and G_2 = (V_2, E_2), such that V_1 = V_2 = {1, 2, ..., n} are isomorphic if there is a one-one, onto function pi: {1, 2, ...., n} rightarrow {1, 2, ..., n} such that for...

Apply the Best-Possible Ordering for Solving a Decision Problem Your task In the Induced Subgraph Isomorphism problem, you are given two graphs G1 = (V1, E1) and G2 = (V2, E2) and you are asked...

Your friend proposes a divide - and - conquer approach to compute a minimum spanning tree of a connected graph G = (V, E). The helper function {G_1, G_2} = subgraphs (G) takes the graph G = (V, E)...

- = (a) The subgraph isomorphism problem is as follows. Given two graphs G1 = (V1, E1) and G2 = (V2, E2), does G have a subgraph that is isomorphic to G2? (Two graphs are isomorphic if there exists a...

Q4 6 Points For the following simple graphs G1 = (V1, El) and G2 = (V2, E2) (described by their vertex and edge sets) decide whether they are isomorphic. If they are then prove it, and if they are...

The cc interest rate is 2.750%. Here is a table of 11 month European call option prices on a non-dividend paying stock. Strike Call Price 120.00 38.02 121.00 37.62 130.00 30.02 Construct an arbitrage...

Let X and Y be independent binomial random variables with parameters (n, p1) and (m, p2), respectively. (a) Find E (X/n Y/n) (b) Find Var (X/n Y/n) (c) Show that (x/n Y/n) ~ N (E(Y/n Y/n), Var...

The FASB requires all financial decision makers to adhere to a code of professional conduct

A presentation to the CEO, with the following: PowerPoint slide deck consisting of no more than 6 slides , including the cover slide. Include the most critical aspects of your proposal - those that...

=+ 11. You read in a newspaper that the nominal interest rate is 12 percent per year in Canada and

=+10. Traveling in Mexico is much cheaper now than it was ten years ago, says a friend. Ten years ago, a dollar bought 10 pesos; this year, a dollar buys 15 pesos. Is your friend right or wrong?...

=+ a. Using the Fisher equation (discussed in Chapter 5), what can you infer about expected infl ation in Canada and in the United States?