The solution to the Dirac equation (eigenspinor ) for positive energy is

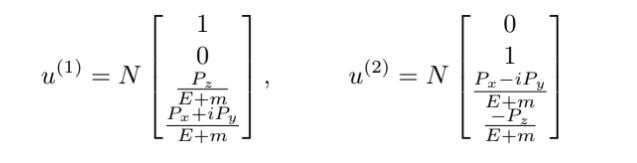
with N =√E+m. It can be seen that an eigenvalue has two eigenspinors, which means there is a decline in the eigenvalue (energy).
This shows that there are other quantities that are commuting with Hamilton but has different eigenvalues between u(1) and u(2).

You might think that u(1) describes a particle with spin up while u(2) particles with spin down. But that case is not correct. You can easily show that u(1) is not an eigenspinor of the spin operator S.

Suppose we choose the spin operator

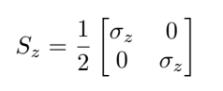
where σz is one of the Pauli matrices and you have to pay attention to it that Sz is a 4×4 matrix. Show that u(1) and u(2) are not the eigenspinor of the operator Sz!

Now if we take the orientation of the particle motion along the z-axis, so it applies Pz > 0, and Px = Py = 0.

a) Denote u(1) and u(2) based on the new motion orientation!

b) Show that these spinors are the eigenspinors of the Sz operator!
c) What is the eigenvalue of the operator Sz for u(1) and u(2)?
 
 

u(1) = N 1 0 P E+m Pr+iPy E+m 0 1 NP-iPy u(2) = N = Etm -P E+m