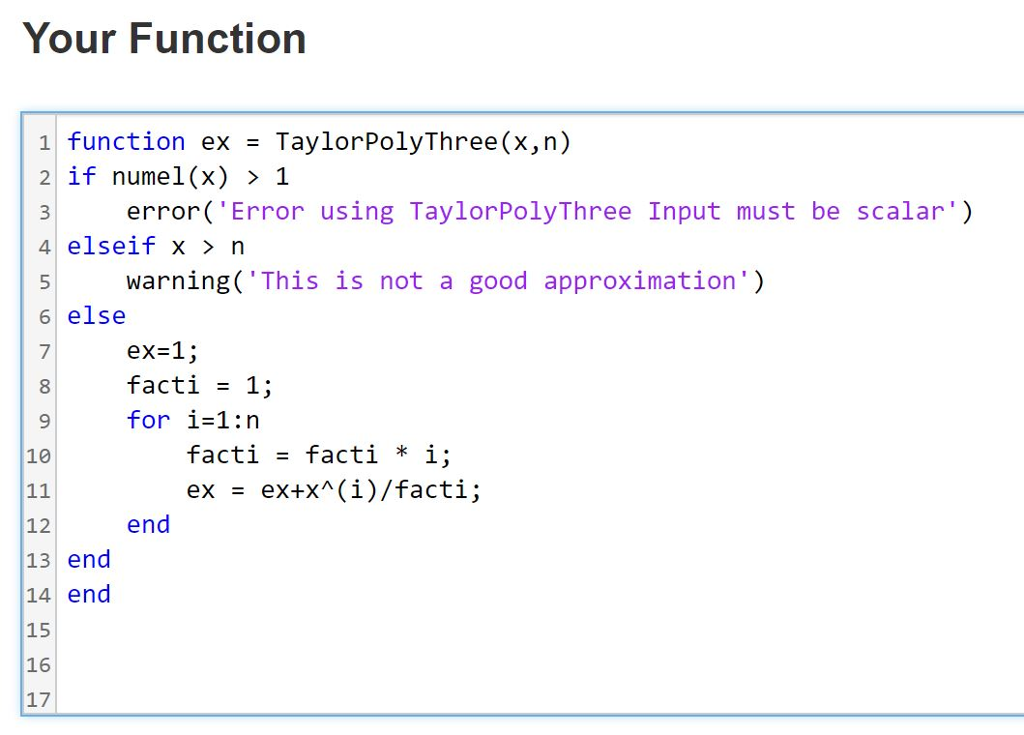
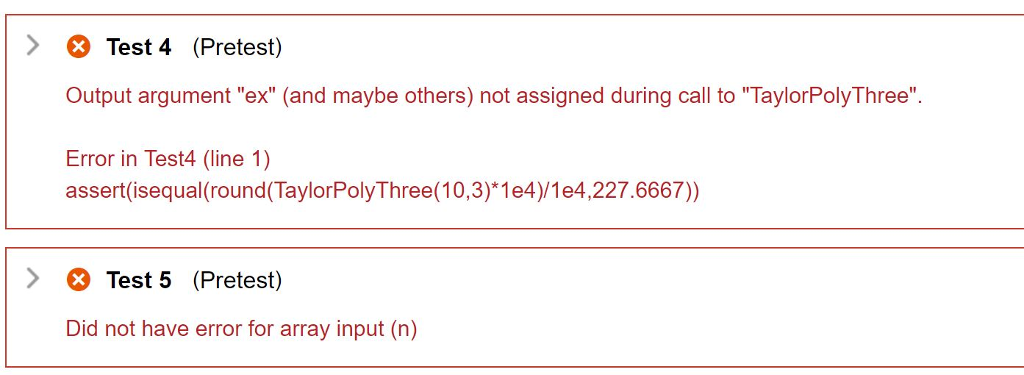
The Taylor polynomial is a powerful tool for approximation The Taylor polynomial of degree n for e*x, for any given x, is: 23!! ending in xn! Write a MA LAB function M-file named Taylo Pol Three. The first input argument to the function should beThe second should b the degre Check if the user enters arrays for n or x. Your code isn't designed to work for these cases. Use the MATLAB error statement..NOT disp Check if the approximated value of e x is within 10% of the real value. Use the MATLAB warning statement to display a message to the use -The above is te same as in Assignment #6. Maybe the third time's the charm! This time, use a for loop to compute the sum Examples: o ayor o nom a n he output ould be he approxima no e this case. Do or used sp TaylorPolyThree(1,3) ans 2.6667 TaylorPolyThree (1,10) ans 2.7183 TaylorPolyThree(I1 3 51,10) Error using TaylorPolyThree Input must be scalar TaylorPolyThree(10,3) Warning: This is not a good approximation Your Function 1 function ex TaylorPolyThree (x,n) 2 if numel(x) 1 3 error( Error using TaylorPolyThree Input must be scalar') 4 elseif x > n 5 warning('This is not a good approximation') 6 else 7 ex 1 fact = 1; for i-1:n 9 10 fact! = fact! * i; end 12 13 end 14 end 15 16 17 Test 4 (Pretest) Output argument "ex" (and maybe others) not assigned during call to "TaylorPolyThree" Error in Test4 (line 1) assert(isequal(round(TaylorPolyThree(10,3)*1e4)/1e4,227.6667)) > Test 5 (Pretest) Did not have error for array input (n)