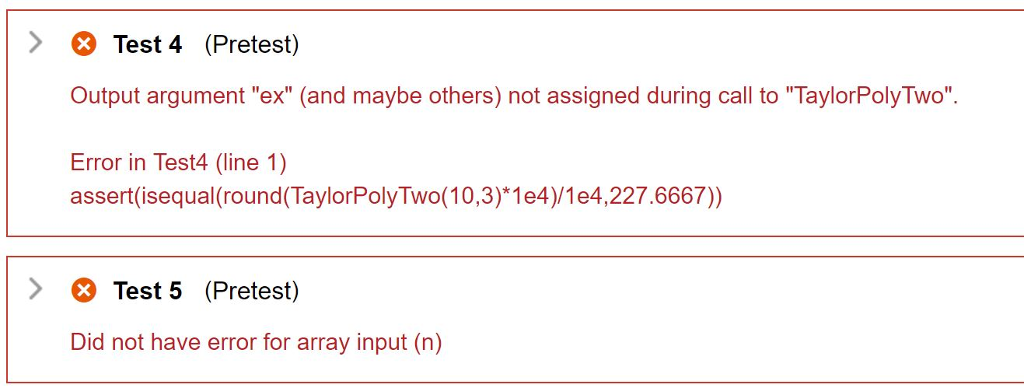
The Taylor polynomial is a powerful tool for approximation The Taylor polynomial of degree n for ex, for any given x, is: 2! 3! 4! 7L n! ending in xAnl Write a MATLAB function M-file named TaylorPolyTwo. The first input argument to the function should be x. The second should be the degree of the Taylor Polynomial, n. The output should be the approximation of e -the above is exactly the same as in Assignment #5. Here is how we will improve it- Add a test to check if the user enters arrays for n or x.Your code isn't designed to work for these cases. Use the MATLAB error statement...NOT disp Add a test to check if the approximated value of eax is within 10% of the real value. Use the MATLAB warning statement to display a message to the user in this case. Do NOT use disp Examples: TaylorPolyTwo(1,3) ans 2.6667 TaylorPolyTwo( 1,10) ans2,7183 TaylorPolyTwo [1 3 5].10) Error using TaylorPolyTwo Input must be scalar TaylorPolyTwo(10,3) Warning: This is not a good approximation 1 function ex TaylorPolyTwo(x,n) 2 3 if numel(x) > 1 4 error ('Error using TaylorpolyTwo Input must be scalar') 5 elseif x> n 6 warning ('This is not a good approximation') 7 else ex-1; factiorial ex -1; 1; 10 11 for i-1:n factiori ex-extxA (i)/factiorial; 12 al afactiorial *i; 13 14end 15 16 end 17 > Test 4 (Pretest) Output argument "ex" (and maybe others) not assigned during call to "TaylorPolyTwo". Error in Test4 (line 1) assert(isequal(round(TaylorPolyTwo(10,3) 1e4)/1e4,227.6667)) > Test 5 (Pretest) Did not have error for array input (n)