^{_{THE THREE FIGUERS SHOUD BE LIKE THIS}}

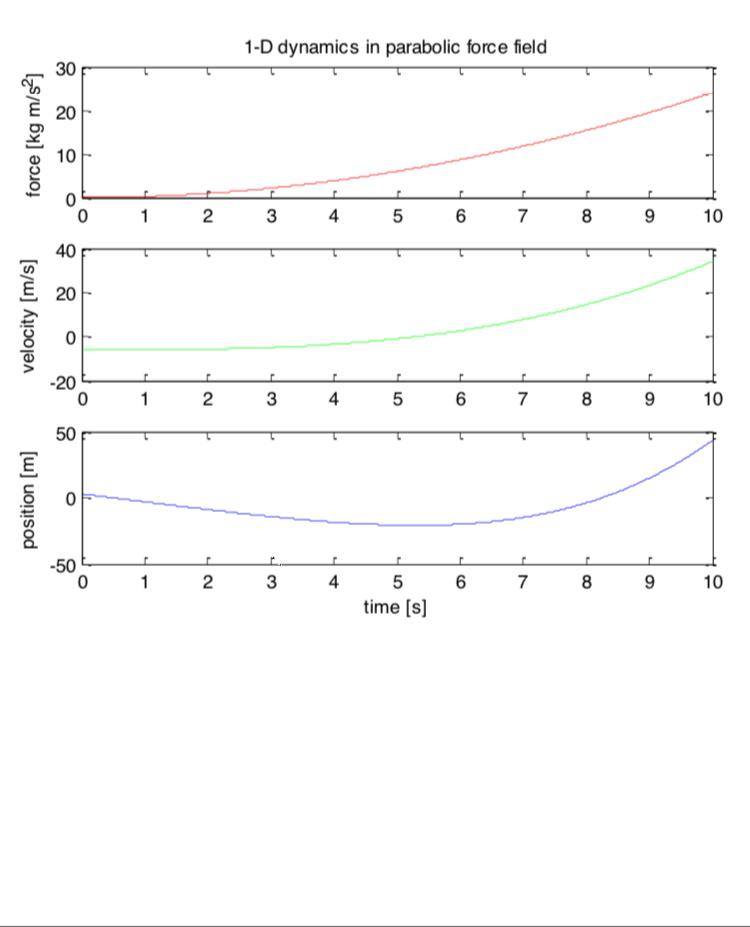
Real dynamical problem. In a real dynamical problem the forces must be given. Then the equations of motion are set up by using Newton's law, which results in a second order differential equation (DE). The solution is obtained by integration. Each of the two sequential integrations yield an arbitrary integration constant: The initial velocity and the initial position. In this exercise we consider the one-dimensional movement of a particle of mass m in a parabolic force field. The above outline is then as follows. Parabolic force field: (t) = At2 Newton's law: (t) ()/m Solve DE: tr 0 3m tt tr 0 12m It is strongly advised that you verify these results! Write a MATLAB position of the particle for times from t0 to time t on one page with proper title and axes labels as sh program as a script file which computes the force, acceleration, velocity and tmax in steps of At. Create three cinput function fou cach ies in the following example. Symbol Value Unit Quantity, Force constant Mass Initial velocity A 0.24 kg m s 2 kg -6 ms Initial position x Maximum timet lime step 10 S max 0.001 s 10 o2 56 10 20 5o tJ