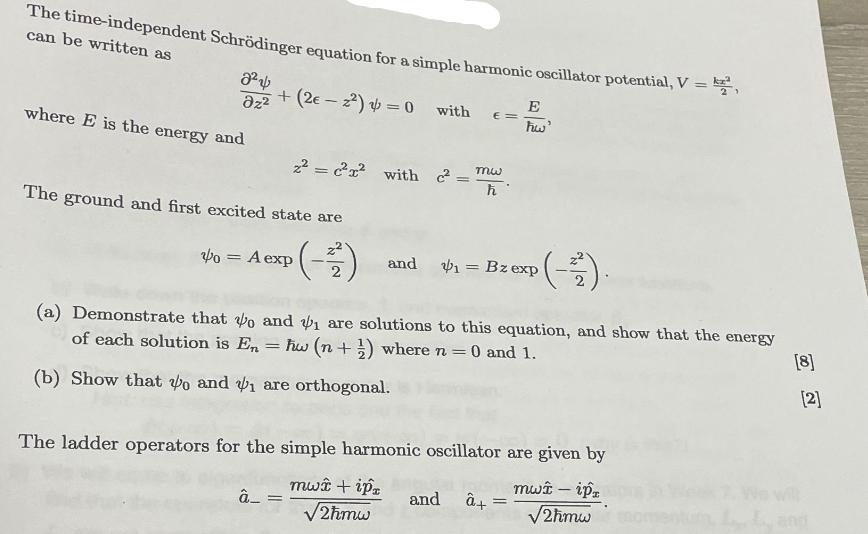
The time-independent Schrdinger equation for a simple harmonic oscillator potential, V= can be written as z2 where E is the energy and +(2-2)=0 with E hw' The ground and first excited state are 0 = A exp _ 2=2 with c = mw 2 = E= and = Bz exp (a) Demonstrate that to and are solutions to this equation, and show that the energy of each solution is En = hw (n +) where n = 0 and 1. (b) Show that to and are orthogonal. The ladder operators for the simple harmonic oscillator are given by mw - ip mw + ipz 2mw 2mw and (-4). + [8] [2]