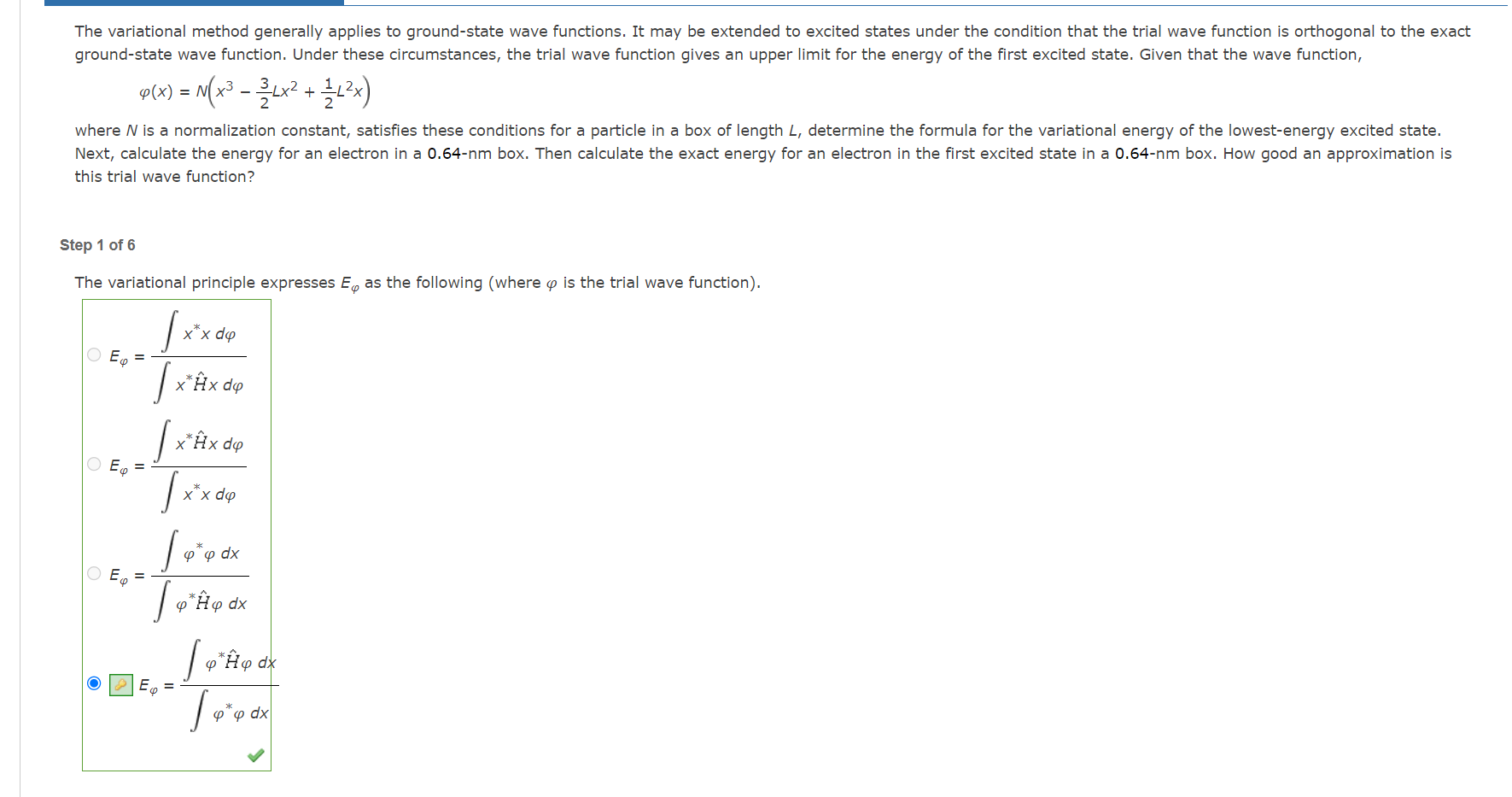
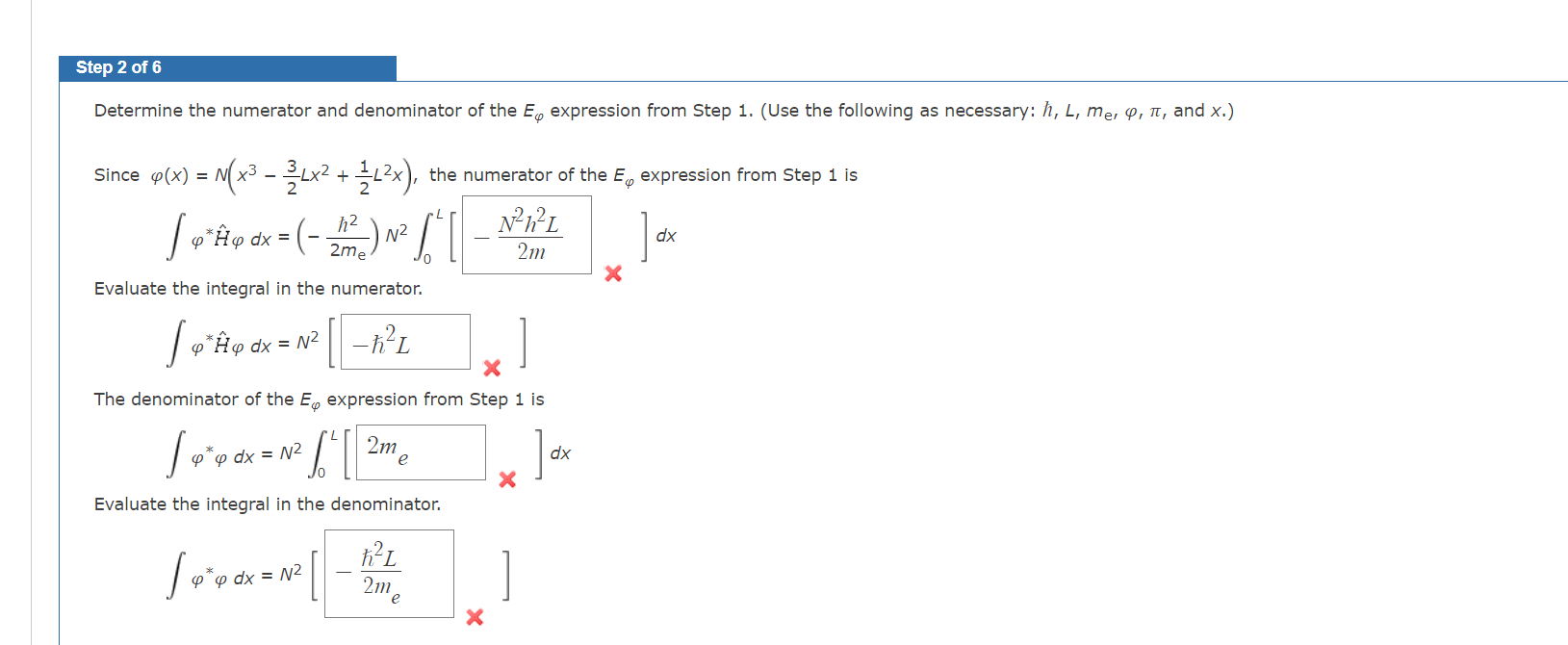
The variational method generally applies to ground-state wave functions. It may be extended to excited states under the condition that the trial wave function is orthogonal to the exact ground-state wave function. Under these circumstances, the trial wave function gives an upper limit for the energy of the first excited state. Given that the wave function, (x)=N(x323Lx2+21L2x) where N is a normalization constant, satisfies these conditions for a particle in a box of length L, determine the formula for the variational energy of the lowest-energy excited state. Next, calculate the energy for an electron in a 0.64nm box. Then calculate the exact energy for an electron in the first excited state in a 0.64nm box. How good an approximation is this trial wave function? Step 1 of 6 The variational principle expresses E as the following (where is the trial wave function). E=xH^xdxxdE=xxdxH^xdE=H^dxdxE=dxH^dx Determine the numerator and denominator of the E expression from Step 1. (Use the following as necessary: h,L,me,,, and x. ) Since (x)=N(x323Lx2+21L2x), the numerator of the E expression from Step 1 is H^dx=(2meh2)N20L[2mN2h2L]dx Evaluate the integral in the numerator. H^dx=N2[2L] The denominator of the E expression from Step 1 is dx=N20L[xdx Evaluate the integral in the denominator. dx=N2[2me2L] The variational method generally applies to ground-state wave functions. It may be extended to excited states under the condition that the trial wave function is orthogonal to the exact ground-state wave function. Under these circumstances, the trial wave function gives an upper limit for the energy of the first excited state. Given that the wave function, (x)=N(x323Lx2+21L2x) where N is a normalization constant, satisfies these conditions for a particle in a box of length L, determine the formula for the variational energy of the lowest-energy excited state. Next, calculate the energy for an electron in a 0.64nm box. Then calculate the exact energy for an electron in the first excited state in a 0.64nm box. How good an approximation is this trial wave function? Step 1 of 6 The variational principle expresses E as the following (where is the trial wave function). E=xH^xdxxdE=xxdxH^xdE=H^dxdxE=dxH^dx Determine the numerator and denominator of the E expression from Step 1. (Use the following as necessary: h,L,me,,, and x. ) Since (x)=N(x323Lx2+21L2x), the numerator of the E expression from Step 1 is H^dx=(2meh2)N20L[2mN2h2L]dx Evaluate the integral in the numerator. H^dx=N2[2L] The denominator of the E expression from Step 1 is dx=N20L[xdx Evaluate the integral in the denominator. dx=N2[2me2L]