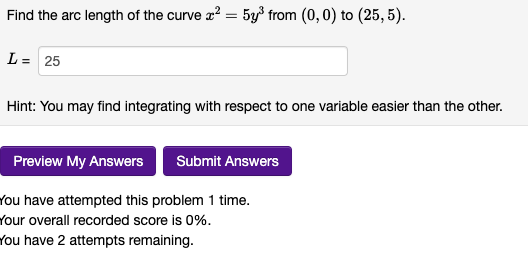
The volume of the solid obtained by rotating the region bounded by about the y-axis can be computed using: a) the method of discs via an integral with limits of integration a = b) cylindrical shells via an integral with limits of integration a = nb = 1 a and b = V = = 1 In either case, a) or b), the volume is V = and B = = 2y, y = 1, x = 0, x = cubic units. ? ? Find the arc length of the curve x = 5y from (0,0) to (25, 5). L = 25 Hint: You may find integrating with respect to one variable easier than the other. Preview My Answers Submit Answers You have attempted this problem 1 time. Your overall recorded score is 0%. You have 2 attempts remaining. The arc length of the curve xy = 20, 1 x 4 can be computed via the integral: S a 1) L OR ii) L = d T sqrt(1-20/(x^2)) sqrt(1-20/(y^2)) de with limits of integration a = 1 dy with limits of integration c = 1 and b = 4 and d = 4